[프로그래머스] 합승 택시 요금
문제 링크 : programmers.co.kr/learn/courses/30/lessons/72413
코딩테스트 연습 - 합승 택시 요금
6 4 6 2 [[4, 1, 10], [3, 5, 24], [5, 6, 2], [3, 1, 41], [5, 1, 24], [4, 6, 50], [2, 4, 66], [2, 3, 22], [1, 6, 25]] 82 7 3 4 1 [[5, 7, 9], [4, 6, 4], [3, 6, 1], [3, 2, 3], [2, 1, 6]] 14 6 4 5 6 [[2,6,6], [6,3,7], [4,6,7], [6,5,11], [2,5,12], [5,3,20], [2,4
programmers.co.kr
플로이드-와샬 알고리즘 또는 다익스트라 알고리즘으로 해결할 수 있는 문제이다.
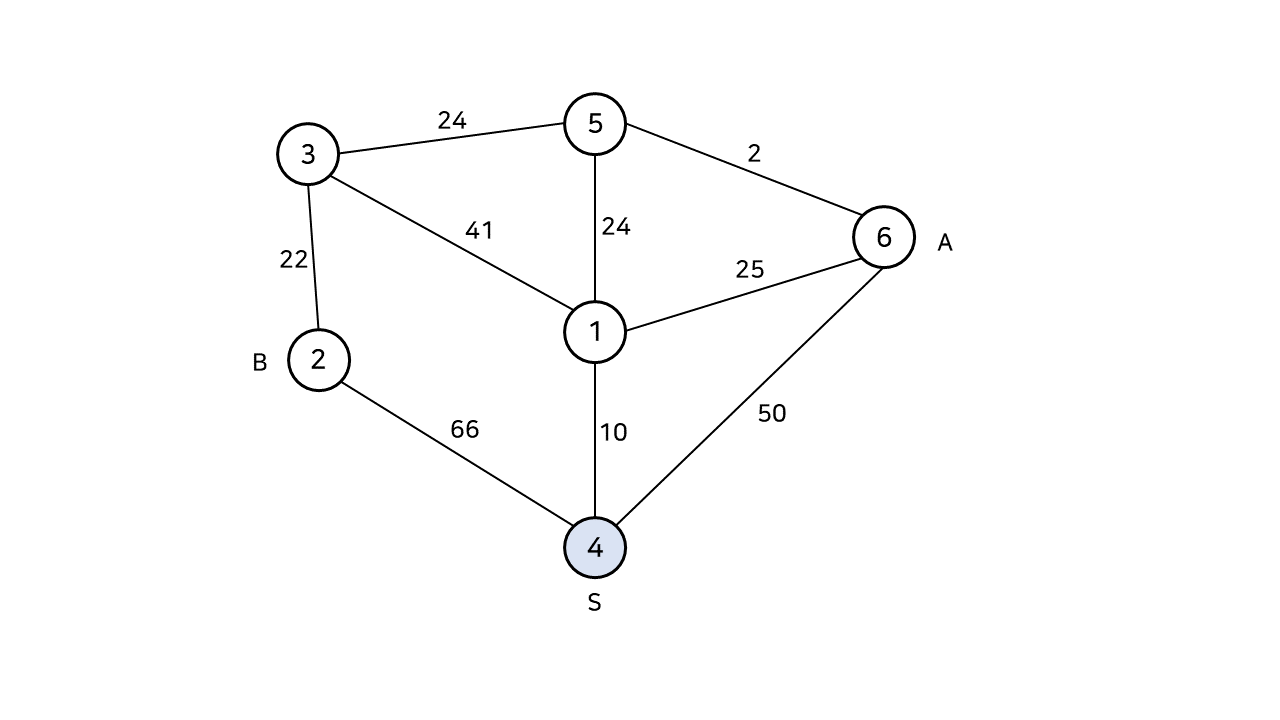
출발 지점에서 A, B의 합승이 끝나는 지점을 K라고 하자. 이 때의 이동거리는 S-K의 최단거리가 될 것이다.
만약 합승해서 가던 A, B가 5번 지점에서 내린다면, 합승한 상태로 이동한 최단거리는 곧 4번 정점에서 5번 정점까지의 최단거리와 같다.
이제 K에서 A, B는 각자의 길을 간다. A는 합승이 끝난 K에서 자신의 집에 해당하는 정점이고, B 또한 그러하다.
만약 5번 지점에서 합승이 끝났다면, A는 5번 정점에서 6번 정점으로 갈 것이고, B는 2번 정점으로 갈 것이다.
이 경우의 최단거리는 5번 정점에서 출발해 2, 6번 정점까지의 최단거리 합이 된다.
즉, 임의의 정점 K에 대해 dist[S][K] + dist[K][A] + dist[K][B]의 최솟값을 구하는 문제이다.
(단, dist[i][j] = i번 정점에서 j번 정점까지의 최단거리)
이를 구하기 위해 다익스트라 알고리즘을 사용할 수도 있으나, 이 풀이에서는 구현이 쉽고 N의 값도 작기 때문에 플로이드-와샬 알고리즘을 사용했다.
[코드]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
|
#include <string>
#include <vector>
#include <algorithm>
#define INF 99999999
using namespace std;
int dist[201][201];
void floyd(int n){
for(int mid = 1; mid <= n; mid++){
for(int s = 1; s <= n; s++){
for(int e = 1; e <= n; e++){
dist[s][e] = min(dist[s][e], dist[s][mid] + dist[mid][e]);
}
}
}
}
void set_dist(int n, vector<vector<int>> fares){
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++){
if(i == j) dist[i][j] = 0;
else dist[i][j] = INF;
}
for(int i = 0; i < fares.size(); i++){
int f = fares[i][0];
int s = fares[i][1];
int w = fares[i][2];
dist[f][s] = w;
dist[s][f] = w;
}
}
int solution(int n, int s, int a, int b, vector<vector<int>> fares) {
int answer = INF;
set_dist(n, fares);
floyd(n);
for(int i = 1; i <= n; i++){
if(dist[s][i] == INF) continue;
if(dist[i][a] == INF || dist[i][b] == INF) continue;
//i번 지점까지 합승 후, 각자 도착지로 가는 비용
int res = dist[s][i] + dist[i][a] + dist[i][b];
answer = min(answer, res);
}
return answer;
}
|
cs |