다익스트라 알고리즘 (Dijkstra Algorithm)
[서론]
그래프 최단경로 알고리즘으로, 꽤 자주 보이는 유형이다.
다익스트라 알고리즘은 음수가 아닌 가중치가 있는 그래프에서 한 점으로부터 다른 모든 점까지의
최단 경로를 구하는 알고리즘이다.
[동작 원리]
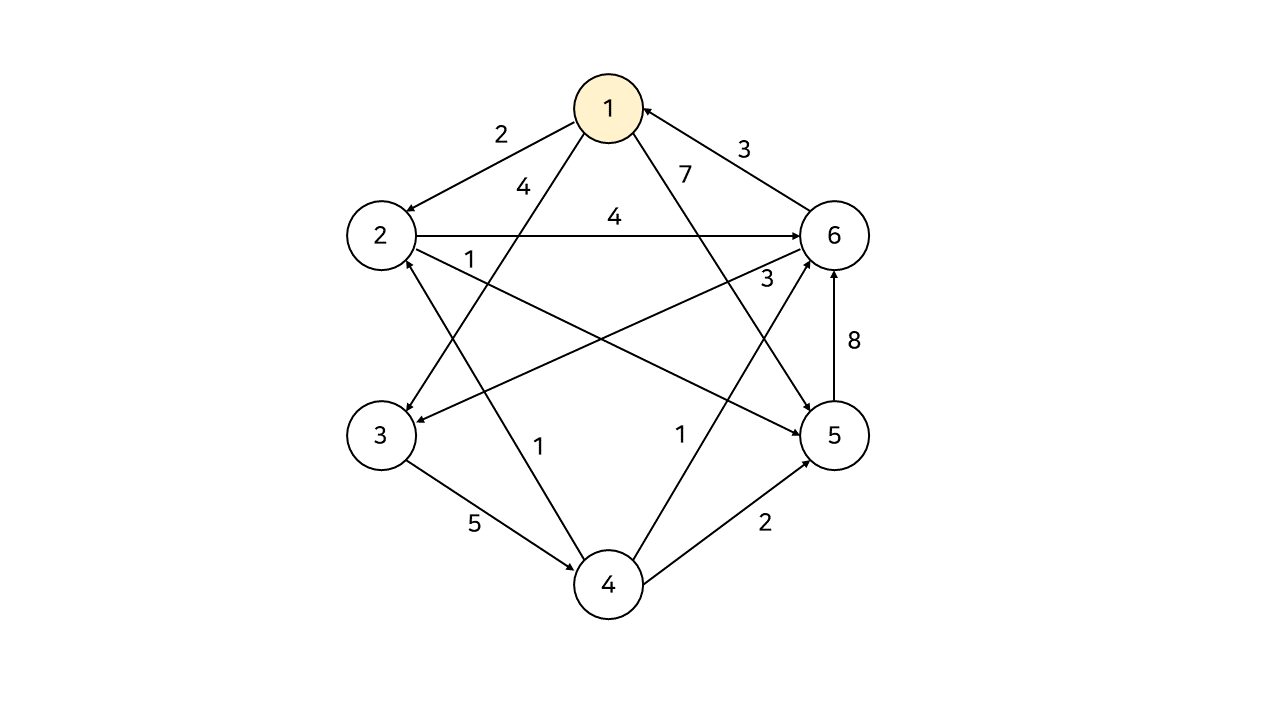
다음과 같은 그래프에서, 1번 노드와 나머지 각 노드 간의 최단거리를 다익스트라 알고리즘을 통해 구해보자.

다익스트라 알고리즘은 위와 같은 상태에서 시작한다.
테이블의 값은 출발 노드로부터 해당 노드까지의 최소 가중치 합을 의미하며,
테이블의 값이 INF(무한대)라면 해당 노드와 연결되어 있지 않다는 의미이다.
아직은 1번 노드만 확인했으므로, 다른 모든 노드에 대해 INF가 기록된 모습이다.

출발 노드로부터 인접한 각 노드에 대해 테이블에 거리를 기록한다.
예시 그래프에서는 출발 노드 1이 2, 3, 5와 인접하므로, 테이블의 2, 3, 5번 칸에 edge의 가중치를 기록한다.
이는 1에서 출발해 2, 3, 5번 노드로 가는 최소 가중치가 2, 4, 7로 현재까지 확인되었다는 의미이다.

다음으로, 이전 과정에서 테이블에 기록한 가중치 중 가장 최소 가중치를 가지는 노드를 선택한다.
여기서 선택한 노드는 더이상 출발 노드로부터의 가중치가 변하지 않는다. 즉, 2의 가중치 2는 고정된다.
다익스트라는 음의 가중치가 없는 그래프에서만 사용하므로, 선택되지 못한 다른 모든 노드는
어떤 경로를 타더라도 절대로 선택한 노드까지의 가중치보다 작아질 수 없기 때문이다.
선택한 노드에 대해 그 노드와 인접한 노드들의 가중치를 갱신한다.
위 그림에서는 1->5 의 가중치가 7이었지만, 1->2->5의 가중치가 3이므로 더 작은 값으로 갱신했다.
기록하는 가중치는 (간선의 가중치 + 2번 노드의 최소 가중치) 임을 주의하자.

최소 가중치 노드인 5를 선택하고, 5와 인접한 노드인 6에 대해 가중치 갱신을 하는 그림이다.
기존 5까지의 최소 가중치 경로 1->2->5 에 대해 1->2->5->6의 가중치 11은
1->2->6의 가중치 6보다 크므로, 테이블을 갱신하지 않는다.

다음으로 가중치가 작은 3번 노드를 꺼내고, 인접한 4번 노드의 가중치를 갱신한다.


이 과정을 모든 노드에 대해 반복해주면, 출발 노드인 1번 노드로부터 각 노드까지의 최소 가중치 합을 구할 수 있다.
테이블에서 색칠된 부분이 최소 가중치 합에 해당한다.
[구현_Priority Queue 사용]
위의 동작 원리와 같이 2차원 테이블을 이용해서 구현하면 O(V^2)의 시간 복잡도를 갖는다.
각 노드에 대해 인접 노드들의 가중치를 갱신하고, 그 중 최소 가중치를 갖는 노드를 선택해야 하기 때문이다.
하지만 최소 가중치를 선택하는 과정을 우선순위 큐(Priority Queue)로 구현하여
(이 우선순위 큐는 최소 힙(Min-Heap)으로 사용된다)
다익스트라 알고리즘의 시간복잡도를 O(VlogV)로 줄일 수 있다.
[구현 코드]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
|
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
typedef pair<int, int> p;
const int INF = 99999999;
int startnode = 1;
vector<p> adj[7];
//dist : 가중치 합을 기록, prev : 최소 가중치 경로에서 이전 노드를 기록
int dist[7], prevnode[7];
void dijkstra() {
//(가중치, 노드) 형태로 저장됨
priority_queue<p> pque;
//출발 노드의 가중치는 0으로 시작
dist[startnode] = 0;
pque.push({ 0, startnode });
for (int i = 1; i <= 6; i++)
if(i != startnode) pque.push({ -INF, i });
while (!pque.empty()) {
p cur = pque.top();
pque.pop();
int distval = -cur.first;
int node = cur.second;
if (dist[node] >= distval) {
//현재 기록되어있는 가중치 합보다 큐의 가중치가 더 작은 경우
//즉, 현재까지 찾은 경로보다 더 가중치가 적은 경로를 찾았을 때
//그 노드에 인접한 노드들을 큐에 넣어준다. (이미 찾은 다른 경로들의 가중치도 변할 수 있기 때문)
for (int i = 0; i < adj[node].size(); i++) {
//노드에 인접한 간선들에 대해,
p edge = adj[node][i];
if (dist[edge.first] > distval + edge.second) {
dist[edge.first] = distval + edge.second;
pque.push({ -dist[edge.first], edge.first });
//경로 기록을 위해 갱신
prevnode[edge.first] = node;
}
}
}
}
}
void init() {
adj[1].push_back({ 2, 2 });
adj[1].push_back({ 3, 4 });
adj[1].push_back({ 5, 7 });
adj[2].push_back({ 5, 1 });
adj[2].push_back({ 6, 4 });
adj[3].push_back({ 4, 5 });
adj[4].push_back({ 2, 1 });
adj[4].push_back({ 6, 1 });
adj[5].push_back({ 6, 8 });
adj[6].push_back({ 1, 3 });
adj[6].push_back({ 3, 3 });
for (int i = 1; i <= 6; i++) {
prevnode[i] = startnode;
dist[i] = INF;
}
}
void print_path(int node) {
printf(" [%d번 노드]\n", node);
printf(" 최소 가중치 합 : %d\n", dist[node]);
printf(" [경로]\n %d < ", node);
int cur = node;
while (prevnode[cur] != startnode) {
printf("%d < ", prevnode[cur]);
cur = prevnode[cur];
}
printf("%d \n", startnode);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(NULL);
init();
dijkstra();
for (int i = 1; i <= 6; i++) {
if (i != startnode) print_path(i);
}
return 0;
}
|
cs |
[결과]

경로를 역순으로 출력하려면 재귀 방식을 사용하면 된다.
[연습 문제]
BOJ1753_최단경로 : www.acmicpc.net/problem/1753
1753번: 최단경로
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1≤V≤20,000, 1≤E≤300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1≤K≤V)가 주어진다.
www.acmicpc.net