문제 링크 : www.acmicpc.net/problem/8984
8984번: 막대기
첫 줄에는 막대기의 개수와 수평선 사이의 간격을 나타내는 두 개의 정수 N과 L이 주어진다. 여기서 N은 1 이상 100,000 이하이고, L은 1 이상 1,000,000 이하이다. 그 다음 N 개의 줄에는 각 줄마다 막대
www.acmicpc.net
위쪽 수평선의 한 점과 아래쪽 수평선의 서로 다른 10개의 점을 잇는 막대기가 있는 상황을 가정해 보자.
이들 중 가장 긴 막대기를 선택한다고 해서, 가장 긴 지그재그가 나올지는 알 수 없다.
따라서 이 문제는 그리디 알고리즘이 아닌 다이나믹 프로그래밍으로 접근해야 한다.
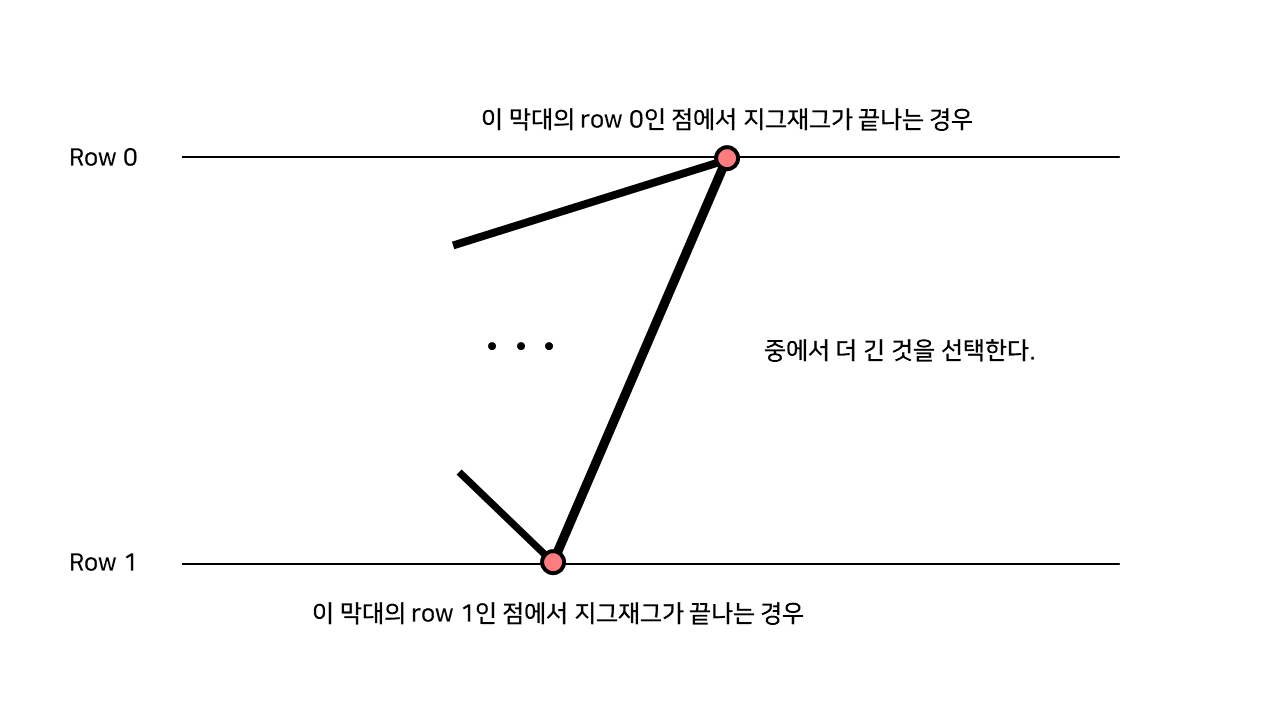
어떤 한 막대에서 지그재그가 끝난 상황을 생각해 보자.
이 때, 맨 마지막 막대를 기준으로 지그재그는 반드시 그 막대기의 위쪽 수평선(row 0) 또는 아래쪽 수평선(row 1) 좌표에서 끝난다.

따라서 k번째 막대기에서 끝나는 지그재그의 최대 길이를 알기 위해서는
k번째 막대의 row 0 좌표 또는 row 1 좌표에서 끝나는 지그재그의 최대 길이를 알아내면 될 것이다.
즉, dp[i][j] = "row j의 i번 좌표에서 끝나는 지그재그의 최대 길이"로 두고 문제를 해결한다.
이를 위해선 반드시 막대들을 한 방향으로만 연결해야 한다는 가정이 필요하다.
그러므로 막대들을 정점 좌표가 작은 순서대로 정렬한 후, 각 막대들을 순서대로 확인하며 dp값을 갱신한다.
[코드]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
|
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef pair<int, int> p;
typedef pair<int, ll>lp;
int n, l;
ll answer = 0;
ll dp[100001][2]; //dp[i][j] : j행의 i번째 정점에서 지그재그가 끝났을 때 최대 길이
vector<int> order[2]; //각 행에 등장하는 위치를 순서대로 저장
vector<p> edges;
void get_dp() {
//반드시 오른쪽으로만 연결한다고 가정한다.
for (int i = 0; i < n; i++) {
p curline = edges[i];
//현재 막대기의 행별 순서를 log시간 내에 탐색
int row0_idx = lower_bound(order[0].begin(), order[0].end(), curline.first) - order[0].begin();
int row1_idx = lower_bound(order[1].begin(), order[1].end(), curline.second) - order[1].begin();
//막대 길이
int len = abs(curline.first - curline.second) + l;
//dp값 갱신
ll row0_temp = dp[row0_idx][0], row1_temp = dp[row1_idx][1];
dp[row0_idx][0] = max(dp[row0_idx][0], row1_temp + len);
dp[row1_idx][1] = max(dp[row1_idx][1], row0_temp + len);
answer = max({ answer, dp[row0_idx][0], dp[row1_idx][1] });
}
}
void init() {
int t, d;
cin >> n >> l;
for (int i = 0; i < n; i++) {
cin >> t >> d;
edges.push_back({ t, d });
order[0].push_back(t);
order[1].push_back(d);
}
sort(edges.begin(), edges.end());
sort(order[0].begin(), order[0].end());
sort(order[1].begin(), order[1].end());
//중복 제거
order[0].erase(unique(order[0].begin(), order[0].end()), order[0].end());
order[1].erase(unique(order[1].begin(), order[1].end()), order[1].end());
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(NULL);
init();
get_dp();
printf("%lld\n", answer);
return 0;
}
|
cs |
'알고리즘 > BOJ 문제풀이' 카테고리의 다른 글
| [DP] BOJ 2618 경찰차 (1) | 2021.01.11 |
|---|---|
| [Floyd] BOJ 13141 Ignition (0) | 2021.01.08 |
| [Dijkstra] BOJ 2211 네트워크 복구 (0) | 2021.01.07 |
| [DP] BOJ 2560 짚신벌레 (0) | 2021.01.07 |
| [Graph] BOJ 3665 최종 순위 (2) | 2021.01.04 |