문제 링크 : www.acmicpc.net/problem/4792
4792번: 레드 블루 스패닝 트리
무방향, 무가중치, 연결 그래프가 주어진다. 그래프의 각 간선은 빨간색 또는 파란색으로 색칠되어져 있다. 이 그래프의 스패닝 트리 중 파란색 간선이 정확히 k개인 것이 있는지 없는지 알아내
www.acmicpc.net
다음과 같은 그래프에서, 파란색 간선을 최소로 사용하는 스패닝 트리를 찾아보자.
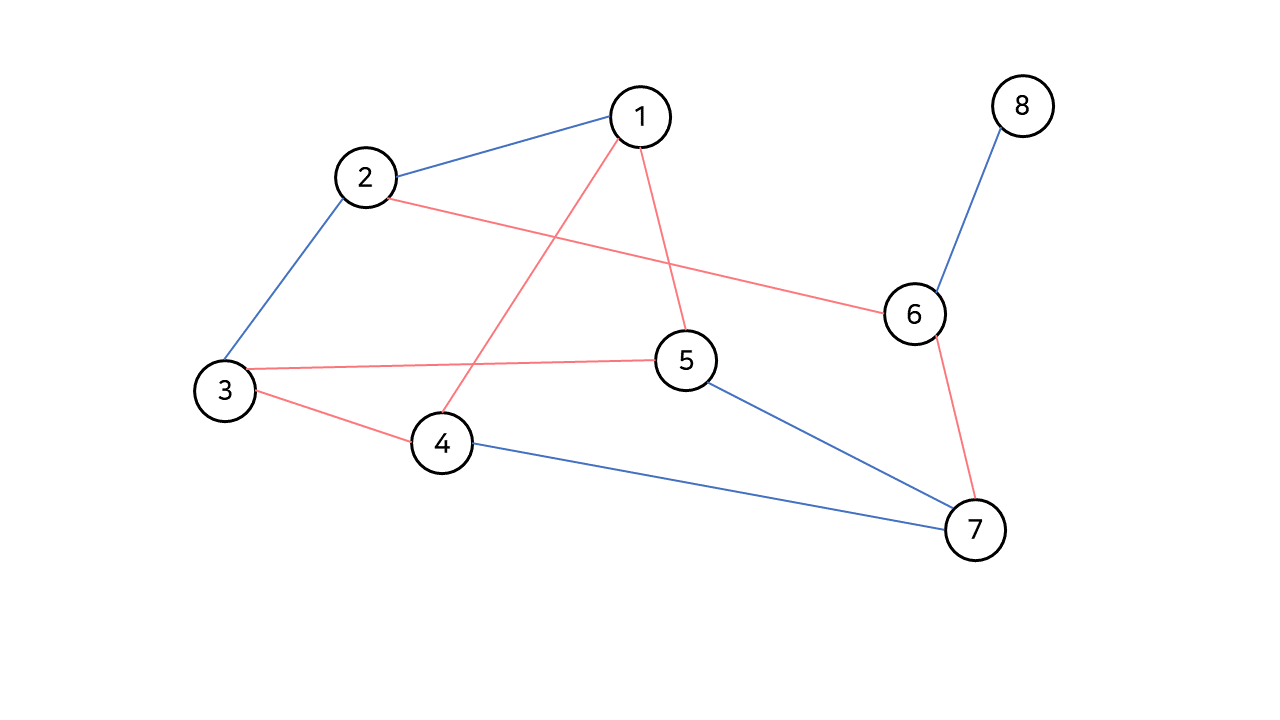

파란색 간선을 최소로 사용했을 때의 스패닝 트리이다.
이는 곧, 예시 그래프에서 스패닝 트리를 구성하기 위해서는 최소 2개의 파란색 간선이 필요하다는 것을 의미한다.
즉 5-7, 6-8의 파란색 간선을 사용하지 않고서는 예시 그래프의 스패닝 트리를 구성할 수 없다.
그렇다면 마찬가지로 이번에는 파란색 간선을 최대로 사용한 스패닝 트리를 구성해 보자.

파란색 간선을 최대로 사용한 스패닝 트리는 곧 빨간색 간선을 최소로 사용한 스패닝 트리와 같다.
위와 마찬가지로, 이 경우 스패닝 트리에 포함된 빨간색 간선은 스패닝 트리를 구성하기 위해 반드시 포함되어야 하는 간선들이다.
따라서, K가 파란색 간선의 최소 개수보다 작거나 최대 개수보다 크다면 그러한 스패닝 트리는 구성할 수 없을 것이다.
하지만, 그 사이에 K가 존재할 경우는 어떻게 확인할 수 있을까?

파란색 간선을 최소로 사용했던 스패닝 트리이다.
여기서 아직 사용하지 않았던 파란색 간선들을 회색으로 표시해보자.

만약 여기서 아무 파란색 간선을 스패닝 트리에 추가하고 싶다면,
스패닝 트리의 조건을 유지하기 위해 이미 스패닝 트리를 구성하고 있던 간선 하나를 지워야 할 것이다.
단, 한 간선을 지우고 원하는 간선을 추가했을 때 스패닝 트리에 사이클이 발생하거나 그래프의 Connected Component가 증가해서는 안 된다. (그래프가 분리되어서는 안 된다)
따라서, 제거하는 간선은 추가할 간선이 잇는 두 정점 간 스패닝 트리 상의 경로 중 하나여야만 한다.
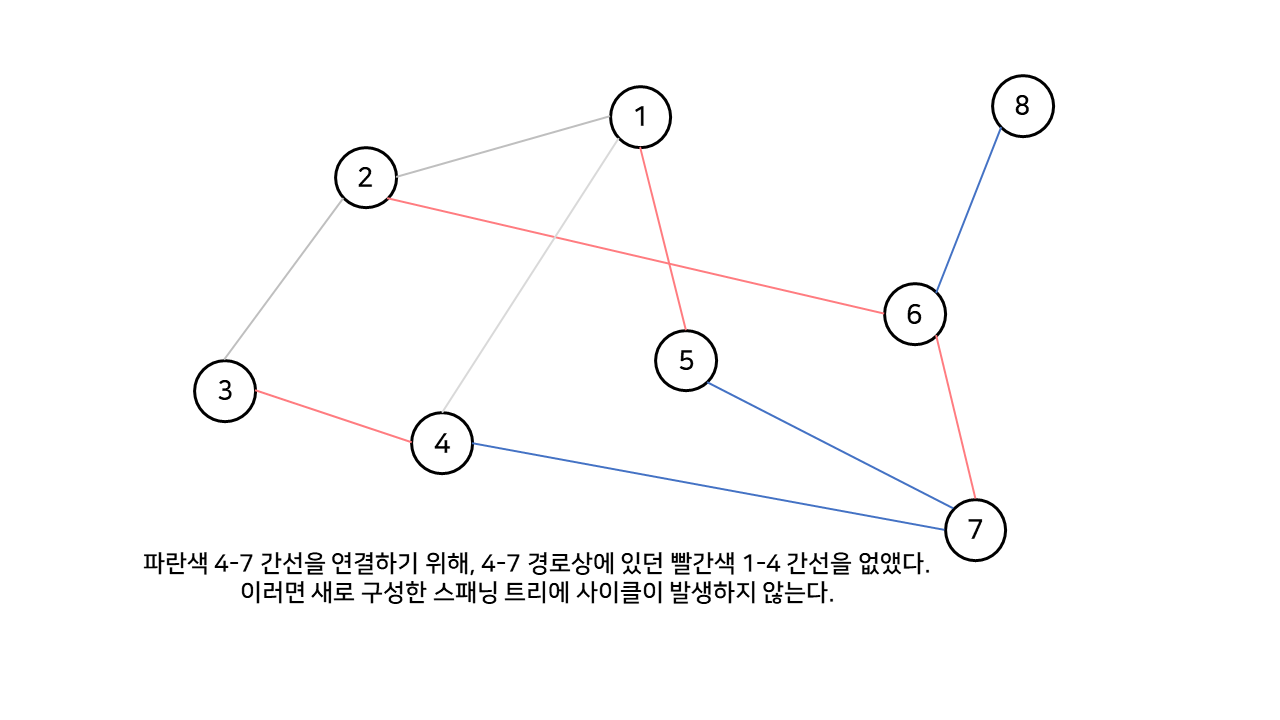
이처럼 4-7 파란색 간선을 추가하기 위해, 스패닝 트리의 4, 7번 노드 간 경로 중 빨간색 간선을 없앤다.
후보 간선은 1-4, 1-5 빨간색 간선이며, 이들 중 아무거나 제거하고 4-7 파란색 간선을 추가해도 여전히 스패닝 트리 구조가 유지됨을 확인할 수 있다.
이를 통해 다음과 같은 사실을 확인할 수 있다.
"스패닝 트리에서 파란색 간선의 최소 개수를 Bmin, 최대 개수를 Bmax라 할 때, Bmin <= k <= Bmax라면 그러한 스패닝 트리는 반드시 존재한다."
위 사실이 성립하는 이유는 지금까지 살펴봤던 내용을 통해 증명할 수 있다.
어떤 스패닝 트리를 구성했을 때, 필수로 들어가야 하는 빨간색 간선을 제외한 모든 빨간색 간선은 파란색 간선으로 대체될 수 있기 때문이다.
[코드]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
|
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
typedef pair<int, int> p;
typedef pair<int, p> e;
int n, m, k, blue_cnt;
int parent[1001]; //Union-Find
vector<e> edges[2];
int find_root(int x) {
if (parent[x] == x) return x;
return find_root(parent[x]);
}
void union_root(int x, int y) {
x = find_root(x);
y = find_root(y);
if (x != y) parent[y] = x;
}
int kruskal(int mode) {
int cnt = 0, mst_val = 0; //mst_val : mst의 가중치 총합, 즉 BLUE의 개수
for (int i = 1; i <= n; i++) parent[i] = i;
for (int i = 0; i < m; i++) {
e cur = edges[mode][i];
int val = cur.first;
int f = cur.second.first;
int s = cur.second.second;
if (find_root(f) == find_root(s)) continue;
union_root(f, s);
mst_val += val;
cnt++;
if (cnt == n - 1) return mst_val;
}
return -1; //mst 구성 불가
}
bool compare(e a, e b) {
return a.first > b.first;
}
void init() {
char t;
int f, s;
cin >> n >> m >> k;
edges[0].clear();
edges[1].clear();
for (int i = 0; i < m; i++) {
cin >> t >> f >> s;
int w = t == 'B' ? 1 : 0;
edges[0].push_back({ w,{f, s} });
edges[1].push_back({ w, {f, s} });
}
sort(edges[0].begin(), edges[0].end());
sort(edges[1].begin(), edges[1].end(), compare);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(NULL);
while (1) {
init();
if (n == 0 && m == 0 && k == 0) break;
int min_blue = kruskal(0);
int max_blue = kruskal(1);
if (min_blue == -1 || max_blue == -1) {
printf("0\n");
continue;
}
if (min_blue <= k && k <= max_blue) printf("1\n");
else printf("0\n");
}
return 0;
}
|
cs |
코드는 파란색 간선의 최소, 최대 개수를 구하기 위해 Kruskal 알고리즘을 사용한다.
파란색 간선의 가중치를 더 높게 잡고 Kruskal 알고리즘을 사용하면 최소 개수를 알 수 있으며,
그 반대로 가중치를 잡으면 최대 개수를 알 수 있다.
'알고리즘 > BOJ 문제풀이' 카테고리의 다른 글
| [DFS] BOJ 1103 게임 (1) | 2021.01.25 |
|---|---|
| [DFS] BOJ 2001 보석 줍기 (1) | 2021.01.25 |
| [Tree/DP] BOJ 2213 트리의 독립집합 (0) | 2021.01.23 |
| [Math] BOJ 8916 이진 검색 트리 (0) | 2021.01.23 |
| [MST] BOJ 10423 전기가 부족해 (0) | 2021.01.19 |