[서론]
크기가 1000인 배열이 있다. 이 배열의 각 원소는 1부터 10까지의 수이다.
이때 i번째 원소부터 j번째 원소까지의 합을 구하고 싶다. 어떤 방법이 좋을까?
가장 먼저 떠오르는 것은 누적합을 이용한 방법일 것이다.

Sk를 Arr[0] ~ Arr[k] 까지의 모든 원소의 합이라 정의할 때,
누적합을 이용해, 구간 (i, j)의 구간합을 Sj - S(i - 1) 로 O(1)에 구할 수 있다.
이 때, Arr의 원소 중 일부가 변경된다면 어떻게 될까?
올바른 구간합을 구하기 위해서는, 누적합을 저장해 놓은 배열을 다시 갱신해야 할 것이다.

배열의 크기가 N이고, 배열값의 변경이 M회 일어날 때 Worst Case에 시간복잡도는 O(NM)이 된다.
이는 N, M의 크기가 어느 정도 커지면 시간 효율 면에서 매우 불리하다.
이렇듯 구간합을 구해야 하는 상황에서, 각 배열의 원소가 자주 변경되는 경우
세그먼트 트리(Segment Tree)를 이용하면 빠르게 구현할 수 있다.
[개념]
세그먼트 트리는 구간을 저장하는 트리이다. 이진 트리(Binary Tree)의 형태로 구현된다.
일반적으로 구간합을 구하는 문제에 응용될 때, 트리의 노드 값은 특정 구간의 구간합이다.
세그먼트 트리는 다음과 같은 특징을 가진다.
■ 최상위 노드(root)는 전체 구간을 나타낸다.
■ 부모 노드가 start - end 의 구간을 저장할 때, mid = (start + end) / 2라 하자.
- 왼쪽 자식은 start - (start + end)/2 구간을 저장한다.
- 오른쪽 자식은 (start + end)/2 + 1 - end 구간을 저장한다.
서론의 예시를 세그먼트 트리로 나타내 보자.

위 그림은 각 노드가 담당하는 구간을 나타낸 것이다.
i-j 로 표현된 노드의 값은 해당 노드가 Arr[i] ~ Arr[j] 의 구간합을 나타낸다는 의미이다.
정의에 따라, 최상위 노드는 구간 전체를 나타내는 0-6이다.
자식 노드들은 부모 노드의 구간을 반씩 물려받아 새로운 부모 노드가 된다.
그림에서 노랗게 색칠된 노드는 리프 노드(Leaf Node)로써, start-end 구간을 담당할 때 start == end 인 경우이다.
이곳에 실제 Arr 배열의 값들이 들어가게 된다. 실제로 서론의 예시에서 저장되는 트리는 다음과 같다.

■ 특정 구간의 합을 알고 싶을 때 (Query)
구하고 싶은 구간을 left-right 로 나타낼 때, 세그먼트 트리에서 원하는 구간의 합을 구해보자.
root 노드부터 시작해 현재 방문한 노드의 구간을 start-end라 할 때, 다음과 같은 경우들이 발생한다.
1. start-end 구간이 left-right 구간에 모두 포함되는 경우
start-end 구간이 구하고자 하는 구간의 부분구간이므로,
start-end 구간합을 그대로 반환하면 된다. (이는 최종 결과의 일부가 된다.)
2. start-end 구간이 left-right 구간을 포함하지 않는 경우
필요없는 구간이므로 합을 구하지 않는다.
3. start-end 구간이 left-right 구간의 일부를 포함하는 경우
양쪽 자식 노드에 대해 재귀실행한다. 반으로 나눈 구간이 구하고자 하는 구간에 포함될 경우, 1에서 처리된다.
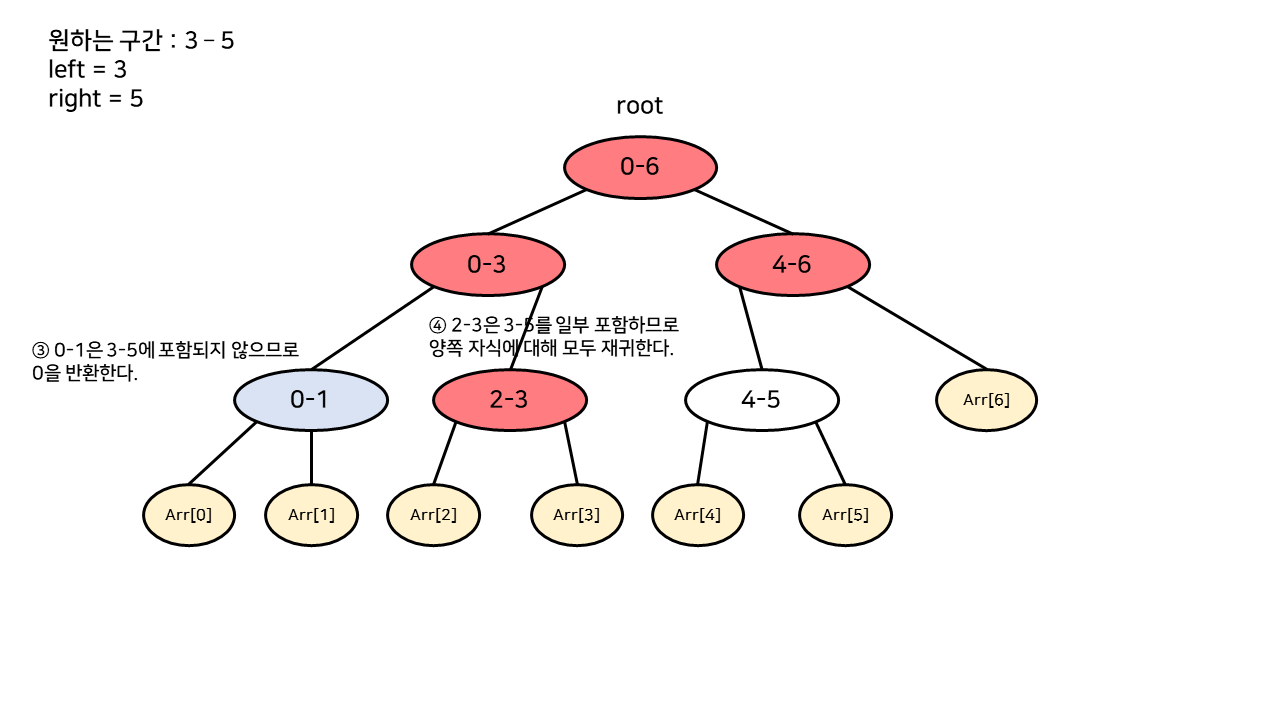
이해를 돕기 위해 상황을 가정해보자. 가령, 3-5 구간의 합을 알고 싶을 때, 구간합을 구하는 과정은 다음과 같다.
붉은색 노드가 실제로 결과값에 더해지는 노드들이고,
파란색 노드는 쿼리의 구간에 포함되지 않아 값을 반환하지 않는 노드들이다.






■ 값의 변경이 일어날 때 (Update)
Arr 배열 내의 i번째 원소를 k만큼 증가시키고자 할 때,
i를 포함하는 모든 구간에 대응하는 노드들의 값을 k만큼 증가시켜줘야 한다.
서론의 예시와 같이 Arr[1]을 3에서 5로 2 증가시키는 과정은 다음과 같다.




[구현 코드]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
|
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
using namespace std;
int arr[7] = { 1, 3, 2, 4, 5, 7, 2 };
int segtree[30];
void create_segtree(int node, int start, int end) {
if (start == end) {
//리프 노드인 경우
segtree[node] = arr[start];
return;
}
int mid = (start + end) / 2;
//왼쪽 자식에 대해 재귀
create_segtree(node * 2, start, mid);
//오른쪽 자식에 대해 재귀
create_segtree(node * 2 + 1, mid + 1, end);
//부모 노드의 값은 양 자식 노드 값의 합이다.
segtree[node] = segtree[node * 2] + segtree[node * 2 + 1];
}
void update_segtree(int node, int start, int end, int target, int val) {
//arr[target]에 val을 더해주는 것에 대응하는 함수
//target에 해당하는 리프 노드와 이를 포함하는 모든 노드들에 대해 val만큼 더해준다.
//구간에 target이 포함되지 않을 경우 종료
if (start > target || end < target) return;
//리프 노드인 경우 val을 더해주고 종료
if (start == end) { segtree[node] += val; return; }
//포함될 경우 트리 값에 val을 더해주고 자식 노드들에 대해 재귀
segtree[node] += val;
int mid = (start + end) / 2;
update_segtree(node * 2, start, mid, target, val);
update_segtree(node * 2 + 1, mid + 1, end, target, val);
}
int query(int node, int start, int end, int left, int right) {
//left-right 구간의 합을 반환하는 함수
//현재 노드의 구간에 left-right 구간이 포함되지 않을 경우 0을 반환
if (start > right || end < left) return 0;
if (left <= start && end <= right) {
//start-end가 left-right에 포함되는 구간일 경우 (즉, start-end가 left-right의 부분구간)
return segtree[node];
}
int mid = (start + end) / 2;
//양쪽 자식에 대해 재귀실행
return query(node * 2, start, mid, left, right) + query(node * 2 + 1, mid + 1, end, left, right);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(NULL);
create_segtree(1, 0, 6);
cout << query(1, 0, 6, 3, 5) << '\n';
update_segtree(1, 0, 6, 1, 2);
for (int i = 1; i <= 15; i++) printf("[%d]%d ", i, segtree[i]);
printf("\n");
return 0;
}
|
cs |
[응용 문제]
BOJ2243_사탕 상자 : www.acmicpc.net/problem/2243
2243번: 사탕상자
첫째 줄에 수정이가 사탕상자에 손을 댄 횟수 n(1≤n≤100,000)이 주어진다. 다음 n개의 줄에는 두 정수 A, B, 혹은 세 정수 A, B, C가 주어진다. A가 1인 경우는 사탕상자에서 사탕을 꺼내는 경우이다. �
www.acmicpc.net
이 문제는 순수하게 세그먼트 트리로 해결이 가능한 문제이지만,
대부분의 세그먼트 트리 응용 문제는 Lazy Propagation과 같이 사용된다.
Lazy Propagation은 다음 포스팅에서 설명한다.
'알고리즘 > 개념' 카테고리의 다른 글
| 벨만-포드 알고리즘(Bellman-Ford Algorithm) (0) | 2020.11.01 |
|---|---|
| 다익스트라 알고리즘 (Dijkstra Algorithm) (0) | 2020.10.21 |
| BFS (Breadth-First Search, 너비 우선 탐색) (0) | 2020.09.29 |
| DFS (Depth-First Search, 깊이 우선 탐색) (0) | 2020.09.29 |
| Bitmask 에 대해 (0) | 2020.09.25 |