[서론]
벨만-포드 알고리즘은 다익스트라 알고리즘과 마찬가지로
한 정점에서 출발하여, 다른 모든 정점에 대한 최단경로를 구하는 알고리즘이다.
(다익스트라 알고리즘 : 4legs-study.tistory.com/21)
하지만, 다익스트라 알고리즘에는 그래프에 음의 가중치가 없어야 한다는 조건이 있었다.
왜일까? 음의 가중치를 가진 간선이 존재한다면, 힙에서 한 정점을 꺼냈을 때
그 가중치 합이 해당 정점에 대한 최소 가중치 합임을 보장할 수 없기 때문이다.
다익스트라 알고리즘은 힙에서 꺼낸 정점에 대해 꺼낸 순간의 가중치 합을 최소로 고정한 후
(음의 가중치가 없다면 다른 어떤 간선을 추가로 지나오더라도 현재 가중치 합보다 작아질 수 없으므로)
다른 정점에 대해 해당 과정을 반복하는데, 음의 가중치를 가진 간선이 그래프에 포함되어 있다면
현재까지 확인된 경로 이후에 다른 간선을 지나와 현재 힙에서 꺼낸 가중치 합보다 작아질 수 있기 때문에
음의 가중치를 가진 그래프에서는 적용될 수 없다.
따라서 이러한 경우에는 벨만-포드 알고리즘을 적용할 수 있다.
다익스트라 알고리즘에 비해 시간적 효율은 떨어지지만, 그만큼 더 많은 그래프들에 대해 정확한 답을 구할 수 있다.
[동작 원리]
벨만-포드 알고리즘은 다음과 같은 생각에서 출발한다.
음의 사이클이 없고 정점이 V개인 그래프에서,
한 정점에서 출발한 다른 정점까지의 최단경로는 많아봐야 V-1개의 간선을 지난다.
즉, 한 번 지난 정점은 다시 지나지 않는다.
(음의 사이클에 대해서는 후술한다.)
따라서, 모든 정점에 대해 V-1번의 반복을 통해 가능한 모든 경로를 탐색하여 정확한 답을 내도록 한다.

다음과 같은 음의 가중치가 포함된 그래프에서, 1번 노드에서 출발하여 각 모든 정점에 대한 최단경로를 구해보자.
[Iteration 1]

처음 iteration은 출발 노드인 1번 노드에 대해 시작한다.
각 간선을 탐색하는 순서는 상관이 없으나, 한 간선에 대해 dist 값이 INF가 아닌 정점이 연결된 경우에만
해당 간선을 탐색하여야 하는 것에 주의하자. (즉, 도달할 수 있는 정점이 연결된 간선에 대해서만 탐색)

1번 노드에서 나가는 3개의 간선에 의해 dist[2], dist[3], dist[4]가 갱신되었다.

2번 노드에서 나가는 간선에 의해 dist[5]가 7로 갱신되었고, dist[3]은 유지되었다.
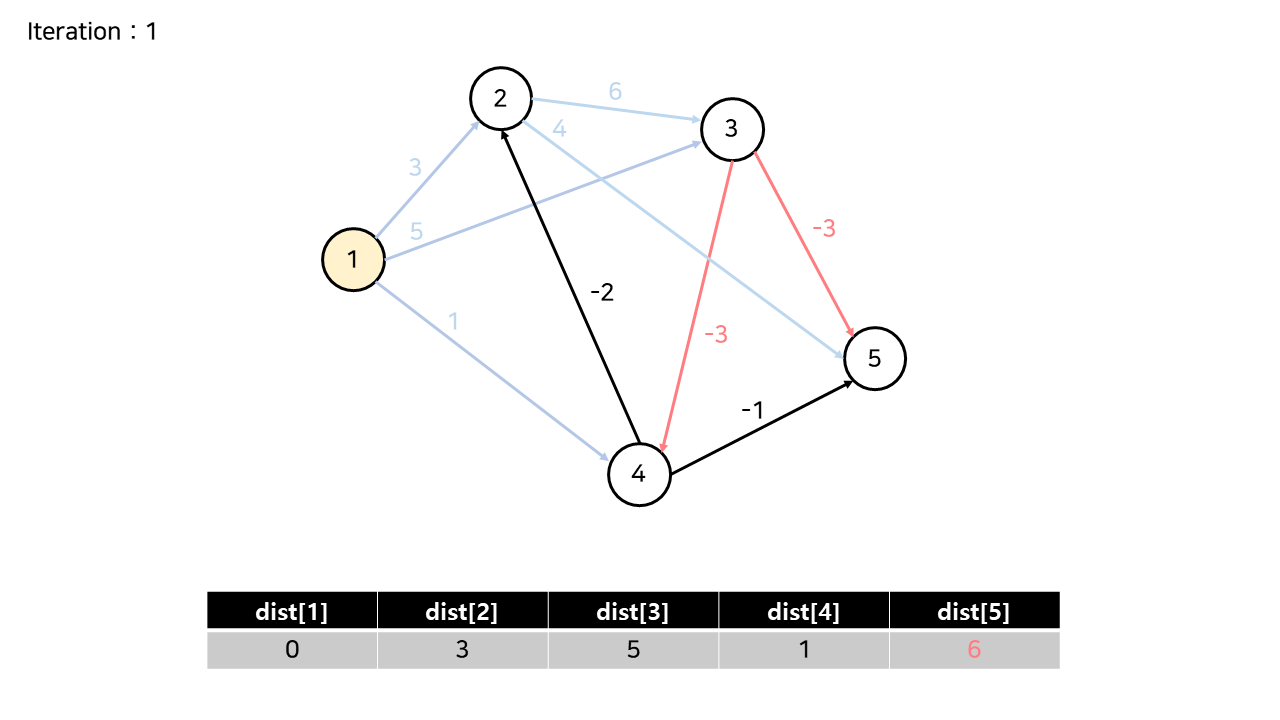
3번 노드에서 나가는 간선들에 의해 dist[5]가 6으로 갱신되었다. (3 + 6 - 3)
dist[4]는 유지되었다.

4번 노드에서 나가는 간선들에 의해, dist[2]와 dist[5]가 갱신되었다.
[Iteration 2]

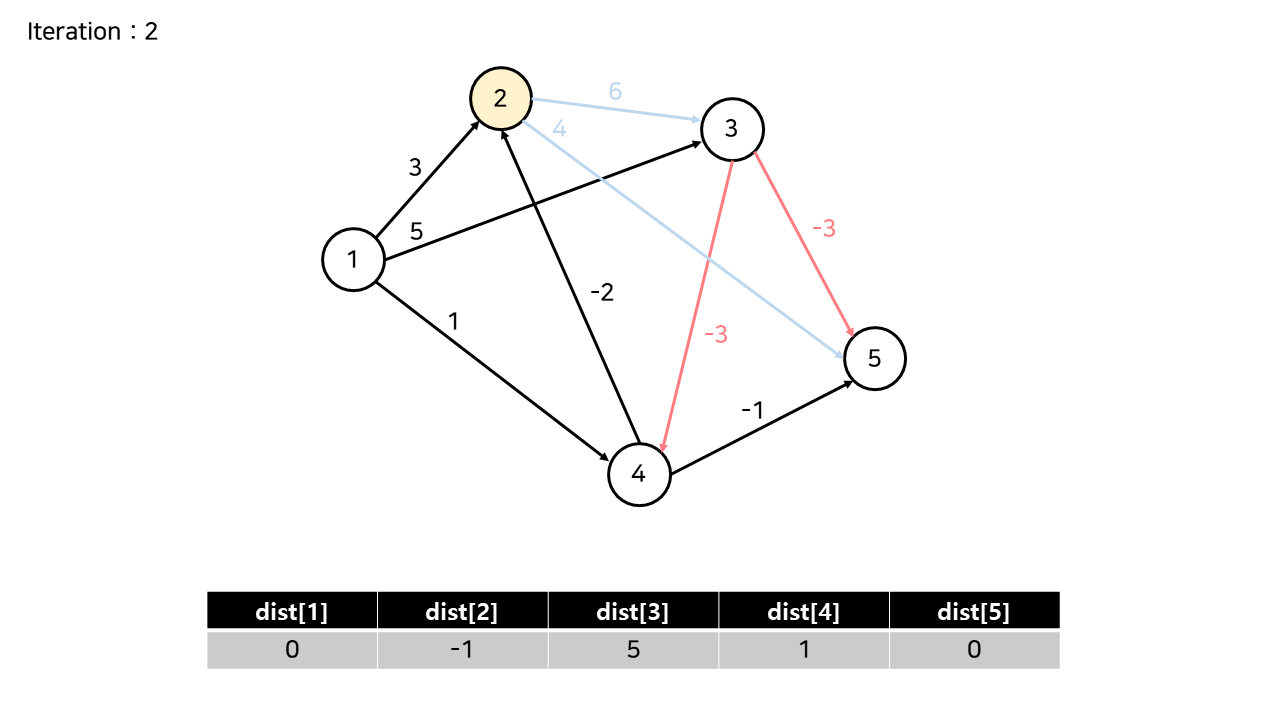
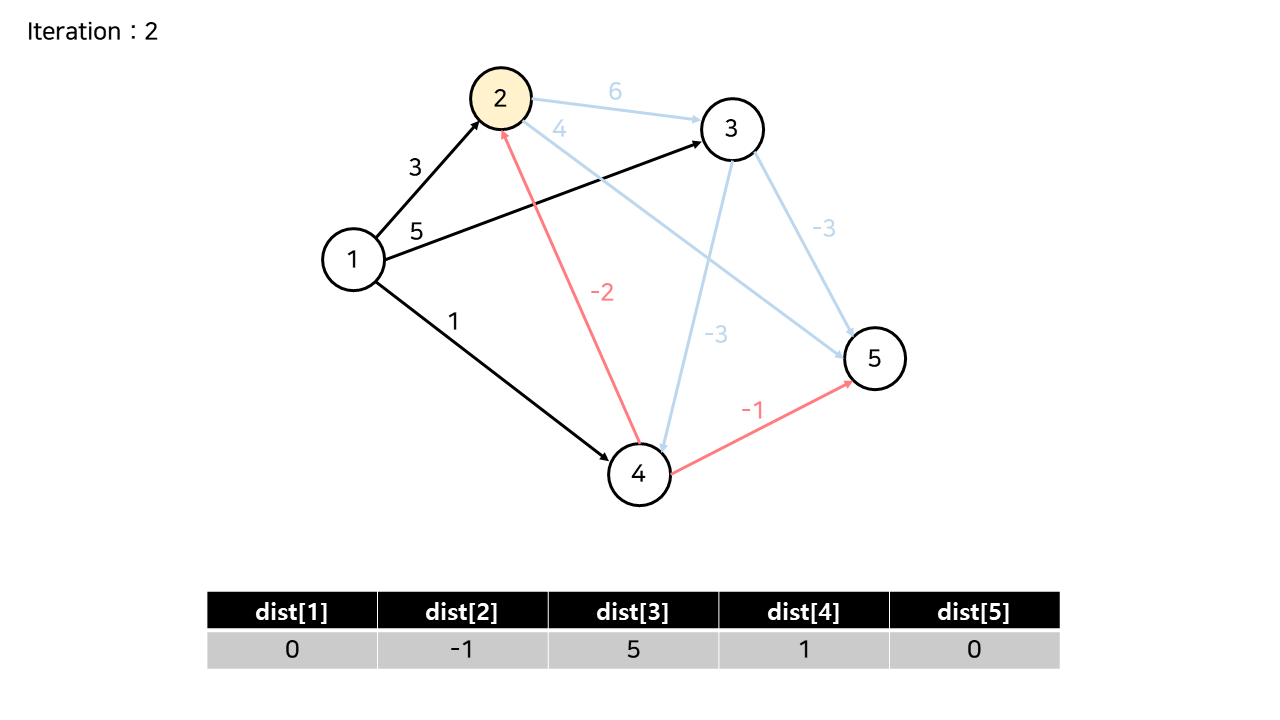

이후의 Iteration에서는, 다른 노드를 순서대로 시작점으로 두고 최단거리를 갱신한다.
(이 예제에서는 더 이상 갱신이 발생하지 않는다.)
Itertaion은 정점의 개수 V에 대해 V - 1번 진행한다.
[음의 사이클]
벨만-포드의 알고리즘은 음의 사이클이 없다는 가정 하에 출발하였다. 음의 사이클은 무엇일까?
그래프의 존재하는 사이클의 가중치 합이 음수인 경우를 말한다.
다음과 같은 경우를 보자.

그림의 2-3-4 사이클을 보자. 이 사이클을 한 바퀴 돌 때마다, 가중치 합이 음수(3 - 2 - 2 = 1)가 되므로
2-3-4 사이클을 무한히 반복하여 지난다면 2, 3, 4, 5번 정점 모두 가중치가 음의 무한대까지 내려갈 수 있다.
벨만-포드 알고리즘은 한 정점으로부터 다른 정점까지의 최단경로는 많아봐야 V-1개의 간선을 지난다는 가정 하에
출발했지만, 위와 같은 음의 사이클이 존재한다면 간선을 V-1개 초과하여 지날수록 더욱 짧은 거리의 경로를
확인할 수 있게 된다.
따라서 벨만-포드 알고리즘에선 위와 같은 음의 사이클을 발견했다면 최단경로가 존재하지 않는다고 결론짓는다.
그렇다면 이 음의 사이클이 존재하는지는 어떻게 확인할 수 있을까?
벨만-포드 알고리즘의 V - 1번까지의 Iteration 이후 더 많은 Iteration을 돌리는 것이다.
V - 1개의 간선보다 더 많은 간선을 통해 최단경로를 구할 수 있다면 음의 사이클이 존재한다고 판단하는 것이다.
따라서, 최소 V번의 Iteration을 통해 벨만-포드 알고리즘은 음의 사이클의 존재 여부도 파악할 수 있다.
벨만-포드 알고리즘의 코드 구현은 아래의 연습 문제를 통해 알아보자.
[연습 문제]
BOJ11657_타임머신 : www.acmicpc.net/problem/11657
11657번: 타임머신
첫째 줄에 도시의 개수 N (1 ≤ N ≤ 500), 버스 노선의 개수 M (1 ≤ M ≤ 6,000)이 주어진다. 둘째 줄부터 M개의 줄에는 버스 노선의 정보 A, B, C (1 ≤ A, B ≤ N, -10,000 ≤ C ≤ 10,000)가 주어진다.
www.acmicpc.net
[Bellman-Ford]BOJ11657_타임머신
문제 링크 : www.acmicpc.net/problem/11657 11657번: 타임머신 첫째 줄에 도시의 개수 N (1 ≤ N ≤ 500), 버스 노선의 개수 M (1 ≤ M ≤ 6,000)이 주어진다. 둘째 줄부터 M개의 줄에는 버스 노선의 정보 A, B,..
4legs-study.tistory.com
'알고리즘 > 개념' 카테고리의 다른 글
| 기본 정렬 알고리즘 (Sorting Algorithm) (0) | 2020.11.20 |
|---|---|
| 플로이드-와샬 알고리즘(Floyd-Warshall Algorithm) (1) | 2020.11.04 |
| 다익스트라 알고리즘 (Dijkstra Algorithm) (0) | 2020.10.21 |
| 세그먼트 트리(Segment Tree) (0) | 2020.10.11 |
| BFS (Breadth-First Search, 너비 우선 탐색) (0) | 2020.09.29 |