효율적인 이진탐색 트리 (Efficient BST)
다음 두 이진탐색 트리를 보자.


첫 번째 BST는 25를 검색하기 위해 6번의 비교가 필요하다. 하지만 두 번째 BST는 3번의 비교로도 검색할 수 있다.
모든 노드를 Search하는 데 비교 횟수를 비교하면, 우리는 두 번째로 제시된 BST가 Search 수행이 더 효율적이라 할 수 있다.
BST가 효율적이기 위해선 가능한 트리의 높이가 최소가 되어야 한다. 그러기 위해선 각 서브트리들이 어느 한쪽으로 치우치지 않고, 균형을 잘 이루어야 할 것이다. 이것이 AVL 트리의 핵심이다.
트리의 균형 (Balance Factor)

우리는 AVL 트리를 사용하기 위해 각 노드마다 균형 인수(BF, Balance Factor)를 둔다.
균형 인수는 한 노드에 대해 왼쪽 서브트리와 오른쪽 서브트리의 높이 차로 정의된다. 이 때 트리의 높이란 트리의 root부터 leaf노드까지의 가장 긴 경로의 길이를 의미한다.
균형잡힌 트리란, 모든 노드에 대해 노드의 BF 절댓값이 1 이하인 트리를 말한다.
트리의 회전 (Rotation)

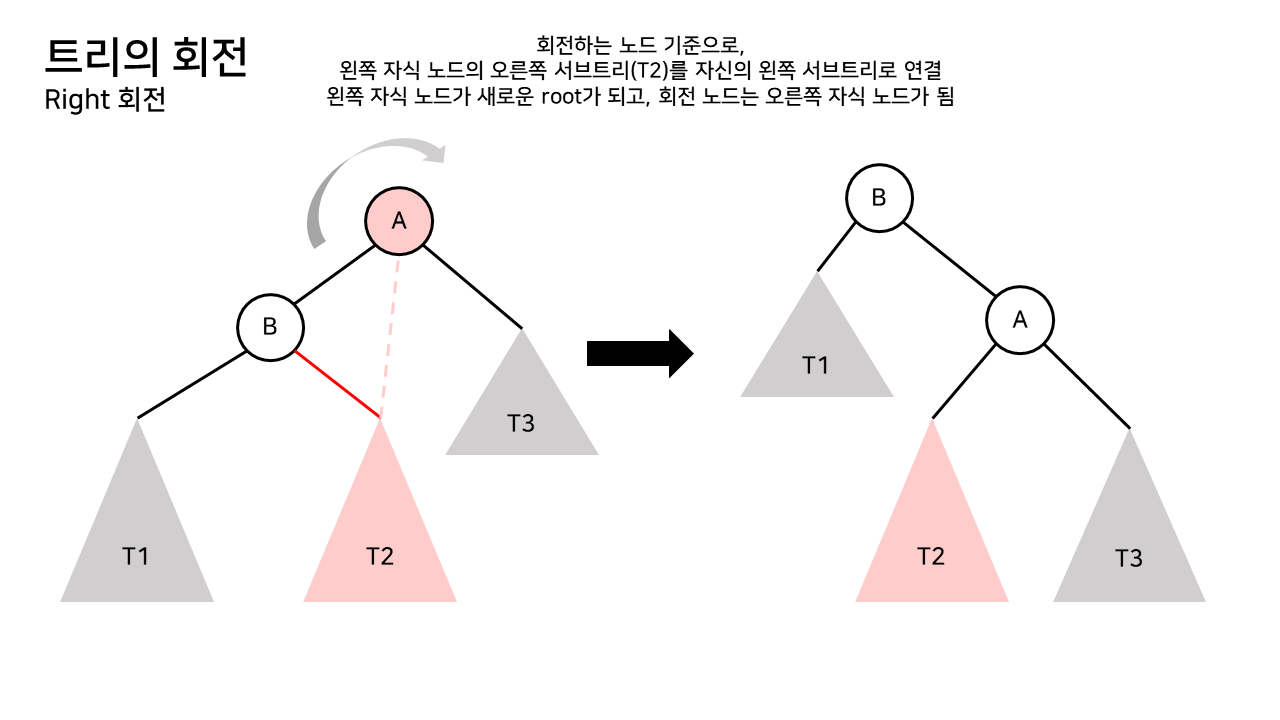
AVL 트리
위에서 살펴본 내용으로 AVL 트리를 어떻게 구현하는지 알아보자.
BST에 원소를 삽입하는 것은 일반적인 BST의 원리와 같다. 하지만 AVL 트리는 균형 인수를 통해 트리의 불균형을 감지한다. 이 경우, 가능한 불균형은 4가지로 나뉜다.
불균형을 감지하였을 때, 트리의 회전을 통해 균형 인수의 절댓값을 1 이하로 유지한다. 이는 삭제에 대해서도 동일하다.




'자료구조' 카테고리의 다른 글
| [자료구조] 트라이 (Trie) (2) | 2020.12.21 |
|---|---|
| [자료구조] Red-Black 트리 (0) | 2020.11.21 |
| [자료구조] 이진 탐색 트리 (Binary Search Tree) (0) | 2020.11.20 |
| [자료구조] 힙 (Heap) (0) | 2020.11.20 |