레드-블랙 트리 (Red-Black Tree)
이전 게시글에서 AVL 트리에 대해 설명하였다. AVL 트리는 효율적인 BST 검색을 위해, 트리를 가능한 균형있게 유지하는 것이 핵심이었다. 하지만 삽입과 삭제의 효율이 좋지 않은 문제가 있다.
레드-블랙 트리의 균형을 맞추기 위한 다른 방법으로 등장한 트리이다.
정의
레드-블랙 트리 BST의 모든 노드가 Black 또는 Red로 칠해진 트리로, 다음과 같은 규칙을 가진다.

RB1. root 노드와 모든 외부 노드(External Node)는 Black Node이다.
(RB1' : 내부 노드로부터 외부 노드로의 포인터는 Black이다. 포인터는 노드를 잇는 간선을 의미한다.)
RB2. root에서 외부 노드까지의 경로는 두 개의 연속적인 Red Node를 가질 수 없다.
(RB2' : root에서 외부 노드로의 경로는 두 개의 연속적인 Red 포인터를 가질 수 없다.)
RB3. root에서 모든 외부 노드로의 경로는 동일한 Black Node 수를 갖는다.
(RB3' : root에서 외부 노드로의 모든 경로는 동일한 Black 포인터 수를 갖는다.)
※ 외부 노드(External Node) : 트리에서 존재하지 않는 노드를 개념적으로 표현한 것이다. 즉, NULL인 노드이다.
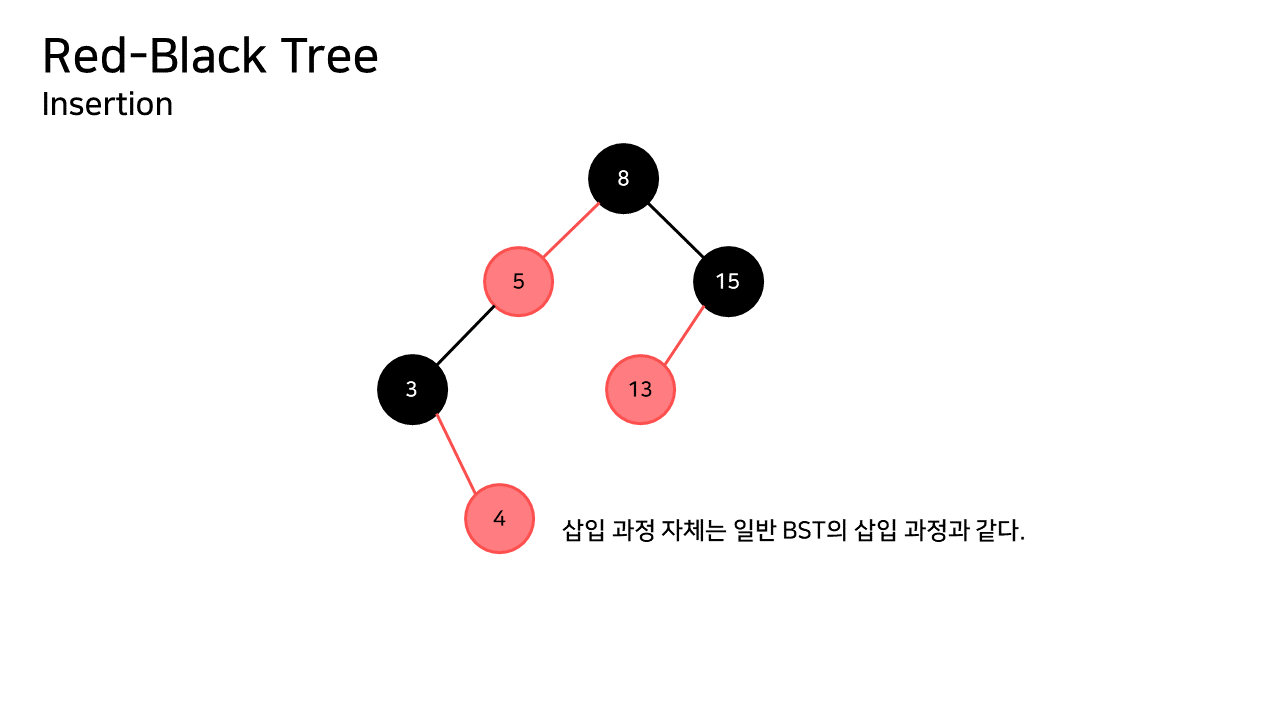
삽입 (Insertion)

Red-Black 트리에서 새로 삽입되는 노드는 기본적으로 Red이다.
RB3 규칙에서 모든 외부 노드까지의 경로는 동일한 수의 Black 노드를 갖는다 하였다. 만약 새로 삽입되는 노드가 Black노드라면, 그 노드와 연결된 외부 노드까지의 경로는 다른 모든 외부 노드의 경로보다 Black 노드 하나를 더 갖게 된다. 따라서, RB3규칙을 위반하게 된다.

Recoloring과 Restructing
Red-Black 트리에서는 연속된 두 개의 Red 노드를 허용하지 않는다 하였다. 따라서 새 Red 노드를 삽입하는 과정에서 연속되는 두 개의 Red 노드가 발견된다면 이를 올바르게 수정해야 할 것이다.


Recoloring은 트리의 구조를 변형하지 않고, 노드의 색만 교체하는 작업이다.
새로 삽입되는 노드의 부모 노드에 대해, 부모 노드의 형제 노드가 Red 노드라면 Recoloring을 진행한다.
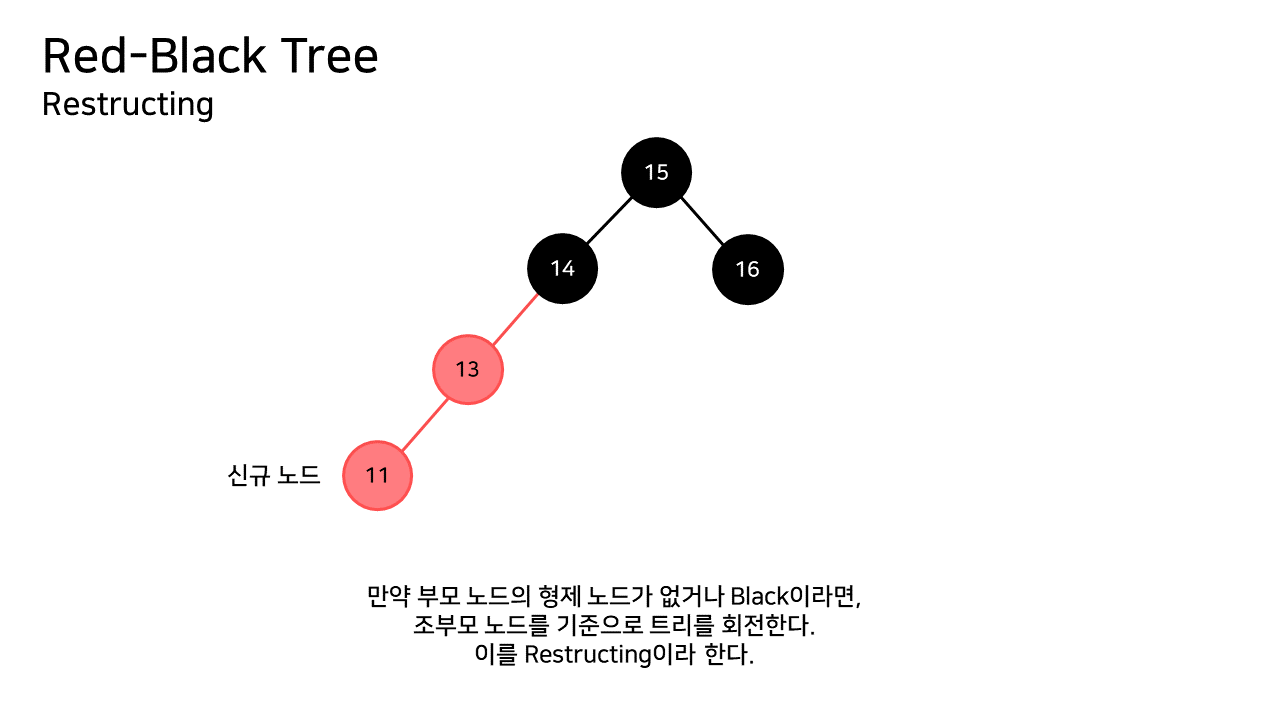

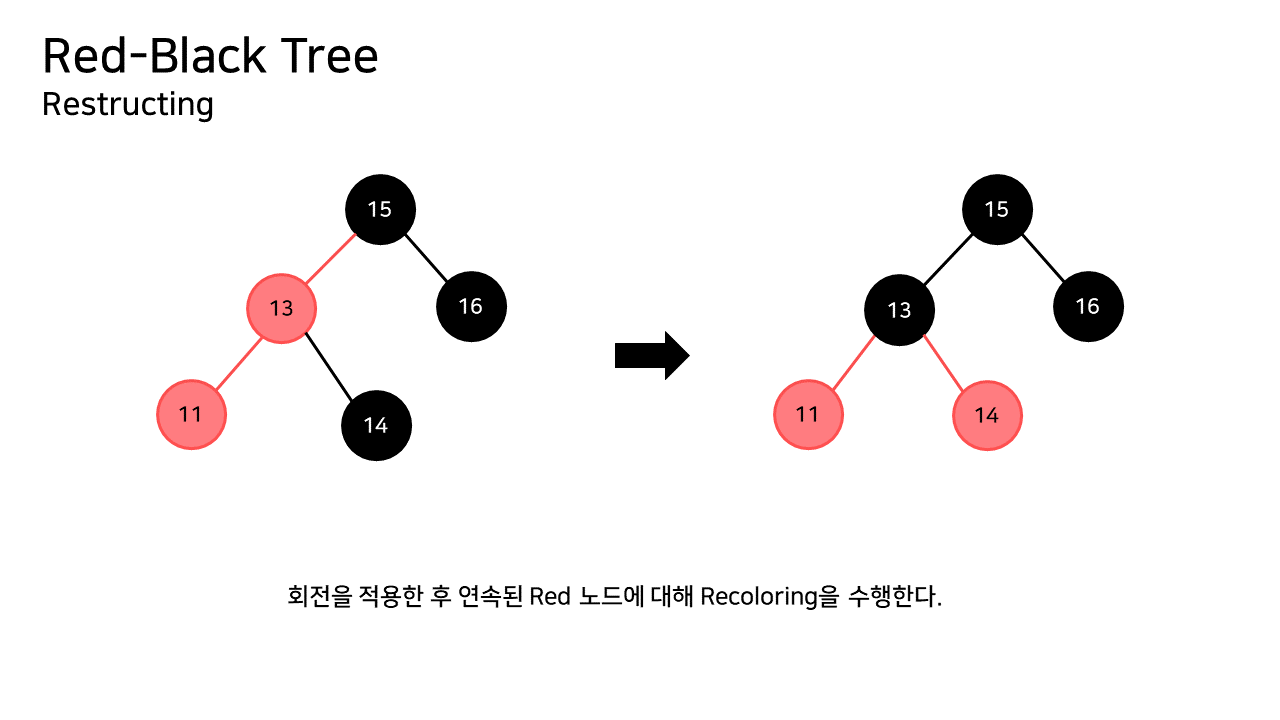
Restructing은 트리의 구조를 변형시켜 RB 규칙들을 유지시키는 작업이다.
새로 삽입되는 노드의 부모 노드에 대해, 부모 노드의 형제 노드가 없거나 Black 노드라면 Restructing을 진행한다.
트리를 회전 후, 남아 있는 Red의 연속은 Recoloring으로 해결할 수 있게 된다.
※ 본 게시글은 『Fundamentals of Data Structures in C』 를 참고하여 작성되었습니다.
'자료구조' 카테고리의 다른 글
| [자료구조] 트라이 (Trie) (2) | 2020.12.21 |
|---|---|
| [자료구조] AVL 트리 (0) | 2020.11.20 |
| [자료구조] 이진 탐색 트리 (Binary Search Tree) (0) | 2020.11.20 |
| [자료구조] 힙 (Heap) (0) | 2020.11.20 |