문제 링크 : www.acmicpc.net/problem/11266
11266번: 단절점
첫째 줄에 두 정수 V(1≤V≤10,000), E(1≤E≤100,000)가 주어진다. 이는 그래프가 V개의 정점과 E개의 간선으로 이루어져 있다는 의미이다. 다음 E개의 줄에는 간선에 대한 정보를 나타내는 두 정수 A, B
www.acmicpc.net
그래프의 단절점이란, 그래프에서 한 정점을 제거했을 때 그래프의 Connected Component가 증가하는 정점을 말한다.
Connected Component는 DFS, BFS 등으로 그래프를 탐색했을 때 한 덩어리로 묶이는 정점들의 집합이라 이해하면 된다. 즉 그래프의 모든 정점을 발견하는 데 실행되는 탐색의 횟수와도 같다.
다음 그래프를 통해 단절점의 특징을 파악해보자.

이 그래프는 현재 Connected Component가 1이다. 시작 정점에 관계없이 한 번의 탐색으로 모든 정점을 발견할 수 있기 때문이다. 이 그래프에서 3번 노드를 없애는 경우를 생각해 보자.
노드를 제거하면, 그 노드와 연결된 모든 간선도 제거된다.

3번 노드를 제거하니 그래프가 총 2 덩어리로 나뉘었다. 즉, Connected Component가 1 증가해 2가 되었다.
따라서 3번 노드는 이 그래프에서 단절점이다.
이번엔 4번 노드를 제거한 경우를 보자.
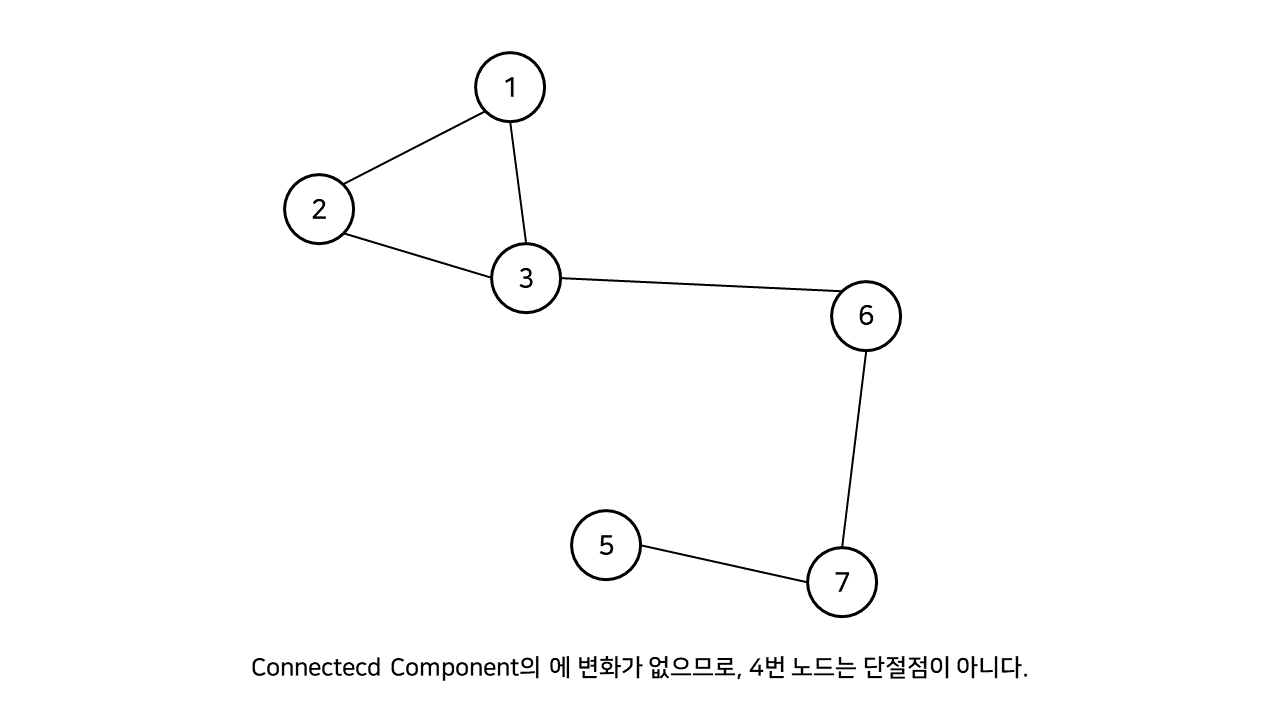
4번 노드를 제거했지만, 그래프는 여전히 한 덩어리로 이루어져 있다. 따라서 4번 노드는 단절점이 아니다.
그렇다면 그래프에서 한 정점이 단절점인지 아닌지는 무엇을 가지고 판단할까?
앞선 예시 그래프에서 3번 노드를 제거했을 때는, 4번 노드에서 1, 2번 노드로 향하는 경로가 없게 된다.
하지만 4번 노드를 제거했을 때는, 5번 노드에서 1 ~ 3 노드로 향할 수 있는 경로가 여전히 존재한다. 즉, 우회로가 존재하는 것이다.
이 우회로의 개념을 이용해, 단절점은 다음과 같은 과정으로 구할 수 있다.
① 임의의 한 정점을 시작으로 그래프 전체를 DFS 탐색한다. 이 때, 각 정점을 방문하는 순서를 기록한다. 또한 탐색을 시작한 노드를 Root이라 하자.
② 현재 탐색하는 방문 순서가 m인 임의의 한 정점 K에 대해, K에서 도달할 수 있는 정점들 중 방문 순서가 가장 빠른 정점을 고른다. (이 과정에 대해서는 후술한다.)
③ 만약 그 정점의 방문 순서가 정점 K의 방문 순서 K보다 작다면, 우회로가 존재하는 것이다. 하지만 그렇지 않을 경우, K는 단절점이 된다.
처음의 예시 그래프에 이를 적용해보자.
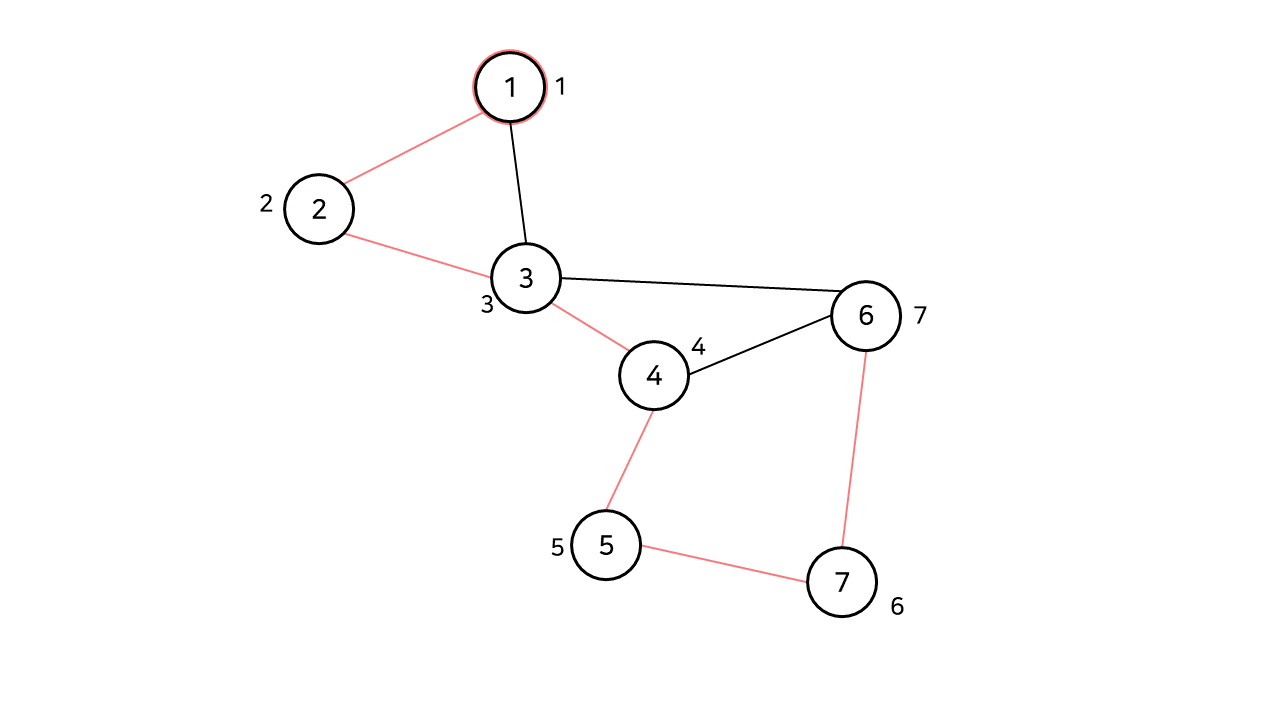
1번 정점에서 DFS를 통한 각 정점의 방문 순서는 다음과 같다.
이제 우리가 찾아냈던 단절점인 3번 노드를 살펴보자.
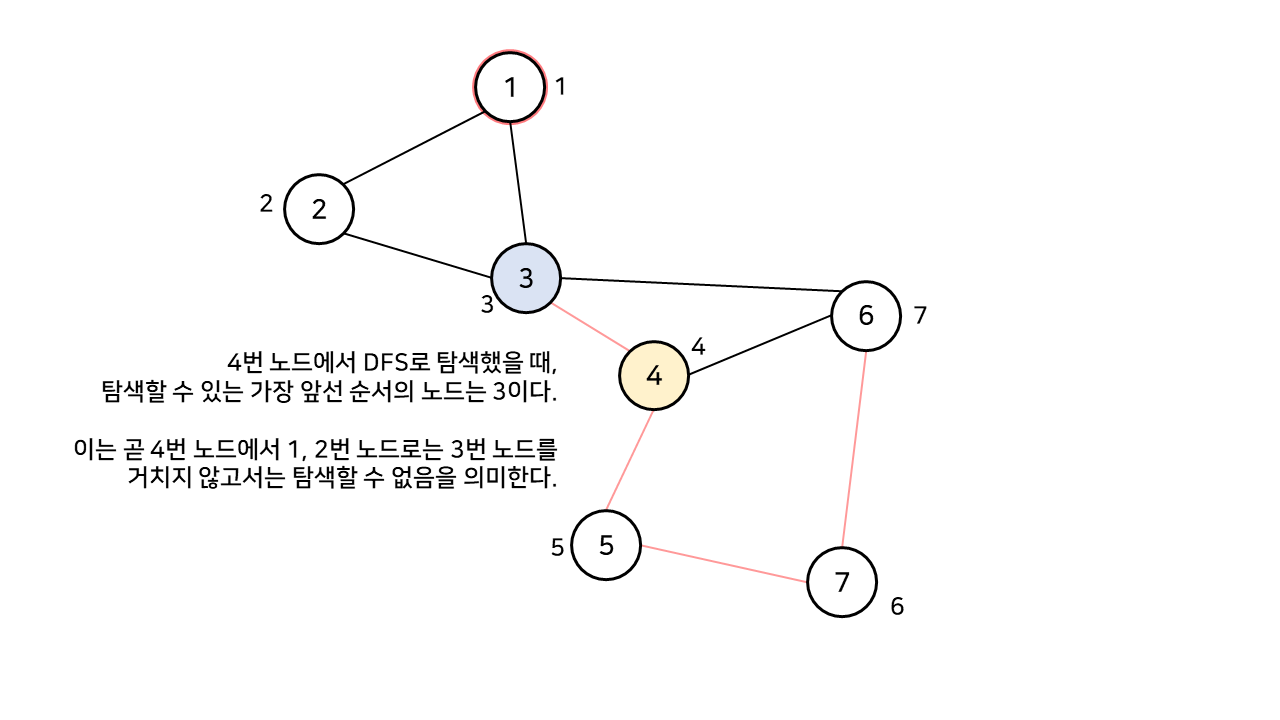
편의를 위해 방문 순서를 먼저 기록했지만, 우리가 3번 노드를 볼 때는 아직 4, 5, 6, 7번 노드는 탐색되지 않은 상태이다.
이제 3번 노드와 연결된 각 노드들에 대해, 그 노드에서 도달할 수 있는 가장 빠른 순서의 정점을 찾는다.
(단, 이미 방문했던 노드를 만난 경우에는 더 탐색하지 않는다.)
1번 노드를 기준으로 하면 2번 노드가 될 것이고, 2번 노드를 기준으로 하면 1번 노드가 된다. 이 둘은 모두 현재 3번 노드의 방문 순서보다 앞서므로, 문제가 없다.
하지만 4번 노드를 기준으로 하면 가장 빠른 순서의 노드는 3번이 된다. 이는 3번 노드의 방문 순서보다 작지 않으므로 3번 노드는 단절점이 된다.
이는 곧 3번 노드를 거치지 않고서는 1, 2번 노드에 도달할 수 없다는 것을 의미한다. 즉, 우회로가 존재하지 않는다.
이번엔 4번 노드를 살펴보자.
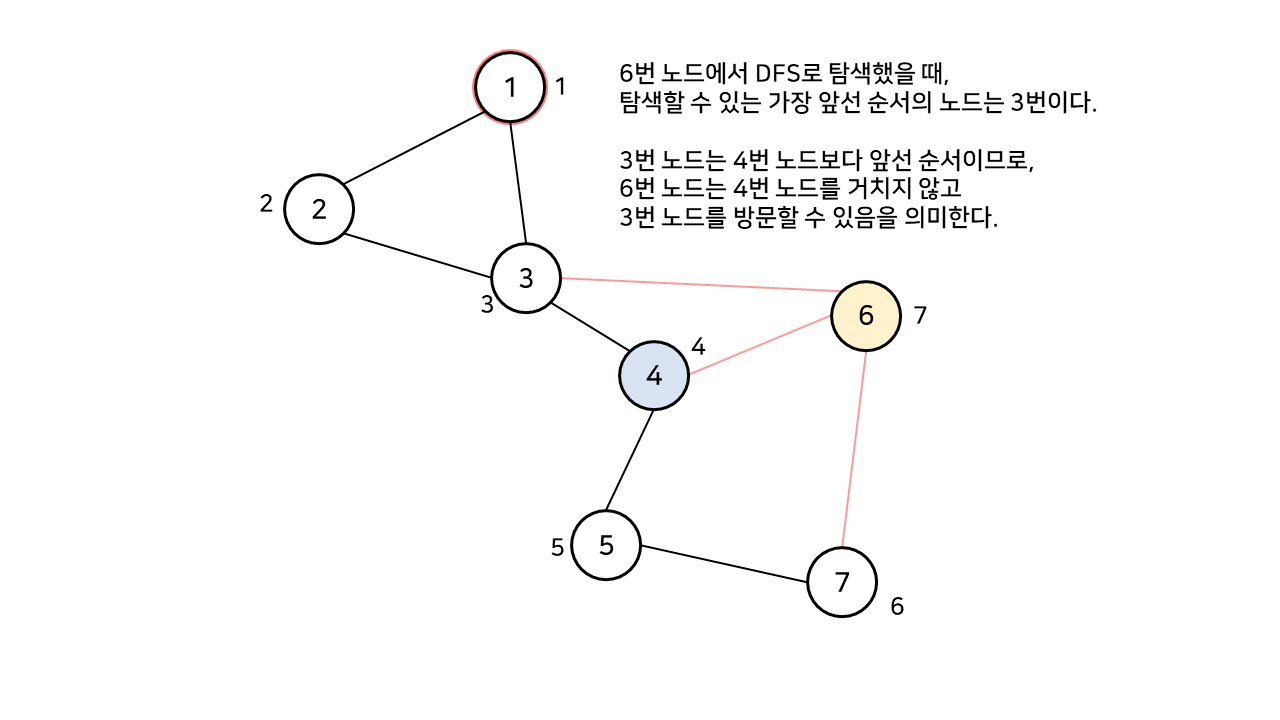
5, 6번 노드에서 이전과 같은 방법으로 방문할 수 있는 가장 빠른 순서의 정점은 3번 노드이다.
3번 노드는 4번 노드보다 앞서는 순서를 갖고 있으므로, 단절점이 되지 않는다.
이는 4번 노드를 거치지 않고서도 3번 노드에 도달할 수 있음을 의미하며, 우회로가 존재한다는 말과 같다.
이 과정을 모든 노드에 대해 진행한다면, 단절점인 정점들을 추려낼 수 있다.
하지만 아직 우리가 단절점으로 확정지을 수 없는 정점이 남아 있다. 바로 최초 탐색을 시작한 Root이다.
Root의 방문 순서는 반드시 1이므로, 그 어떤 노드도 이보다 빠른 순서를 가질 수 없다.
따라서 Root는 별도의 기준으로 단절점임을 파악한다. 다음 그래프를 보자.
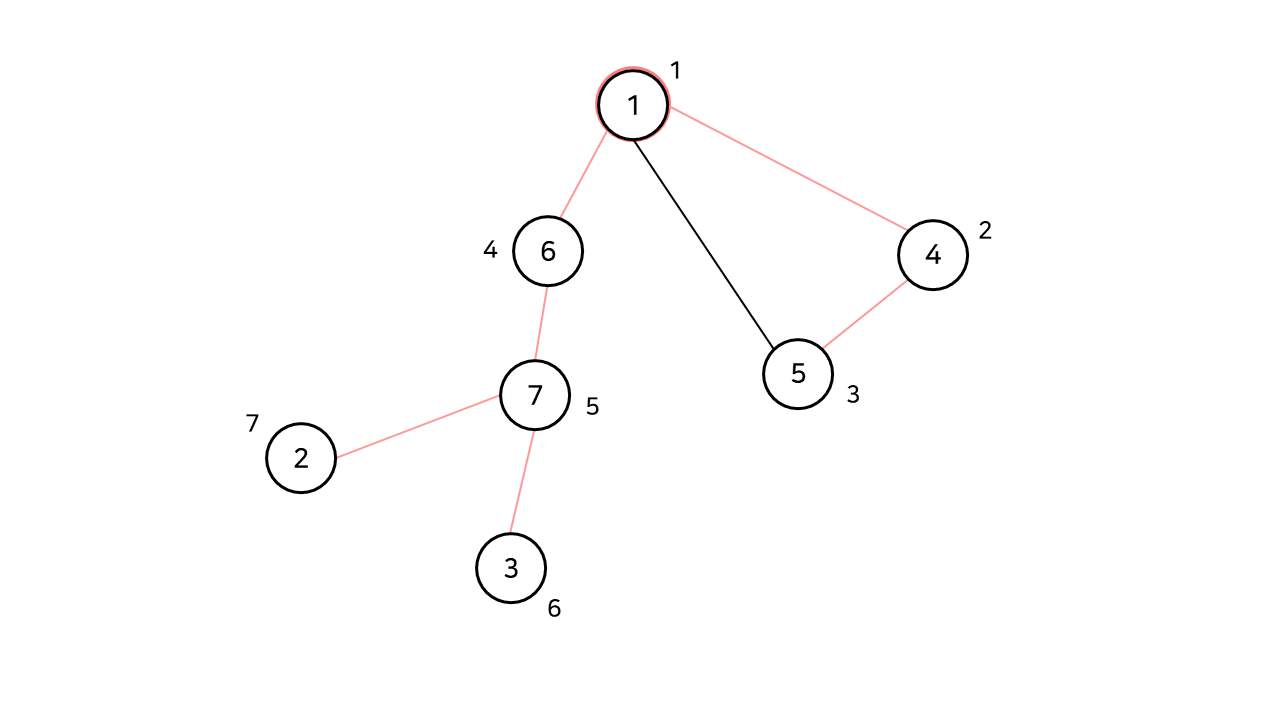
문제의 예제 그래프이다. 이 그래프에서 1번 노드는 단절점이다.
그림의 붉은 간선이 DFS 탐색 순서일 때, 1 -> 4 -> 5에서 탐색이 한 번 종료된 후, 6번 노드부터 탐색이 시작된다.
즉, 붉은 간선을 둘 이상 가졌을 경우 Root 노드는 단절점이 된다.
[코드]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
|
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
typedef pair<int, int> p;
int v, e;
vector<int> adj[10001];
int num = 1, order[10001], cnt = 0;
bool cutting[10001];
int dfs(int node, bool isRoot) {
//반환값 : node부터 dfs로 가장 빨리 발견한 노드의 순서
order[node] = num++;
int degree = 0;
int ret = order[node];
for (int i = 0; i < adj[node].size(); i++) {
int nextnode = adj[node][i];
if (order[nextnode] > 0) {
//이미 순서가 매겨진 노드를 방문했다면, 그 노드의 순서만 기록
ret = min(ret, order[nextnode]);
continue;
}
degree++;
//연결된 노드에 대해, 그 노드에서 탐색했을 때 가장 먼저 탐색한 노드의 order를 반환
int result = dfs(nextnode, false);
if (!isRoot && result >= order[node]) {
//만약 그 반환값이 현재 노드의 순서보다 작은 값을 반환했다면
//현재 노드를 거치지 않고도 그 노드를 탐색할 수 있다는 것을 의미한다.
//따라서 큰 값을 반환했다면, 현재 노드는 단절점이 된다.
cutting[node] = true;
}
ret = min(ret, result);
}
//만약 dfs 탐색을 처음으로 시작한 노드라면, 차수가 2 이상인 경우 단절점이다.
if (isRoot) {
if (degree >= 2) cutting[node] = true;
}
return ret;
}
void init() {
int f, s;
cin >> v >> e;
for (int i = 0; i < e; i++) {
cin >> f >> s;
adj[f].push_back(s);
adj[s].push_back(f);
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(NULL);
init();
for (int i = 1; i <= v; i++) {
if (order[i] == 0) dfs(i, true);
}
vector<int> answer;
for (int i = 1; i <= v; i++)
if (cutting[i]) answer.push_back(i);
printf("%d\n", answer.size());
for (int i = 0; i < answer.size(); i++) printf("%d ", answer[i]);
printf("\n");
return 0;
}
|
cs |
'알고리즘 > BOJ 문제풀이' 카테고리의 다른 글
| [DP] BOJ 2560 짚신벌레 (0) | 2021.01.07 |
|---|---|
| [Graph] BOJ 3665 최종 순위 (2) | 2021.01.04 |
| [Graph] BOJ 15562 네트워크 (0) | 2020.12.31 |
| [Greedy] BOJ 2437 저울 (0) | 2020.12.29 |
| [DP] BOJ 1029 그림 교환 (0) | 2020.12.29 |