[최단거리 알고리즘]
다익스트라 알고리즘 (Dijkstra Algorithm)
벨만-포드 알고리즘 (Bellman-Ford Algorithm)
[서론]
최단거리 알고리즘의 마지막, 플로이드-와샬 알고리즘(이하 플로이드 알고리즘)이다.
플로이드 알고리즘은 그래프에서 모든 정점에서 다른 모든 정점까지의 최단거리를 구하는 알고리즘이다.
그래서 이전까지의 최단거리 알고리즘과는 다르게 dist배열이 처음부터 2차원 배열 형태이다.
벨만-포드 알고리즘과 마찬가지로 음의 가중치가 존재하는 그래프에서도 사용 가능하며,
음의 사이클이 존재하는 경우 최단거리를 구할 수 없다.
[동작 원리]
플로이드 알고리즘은 출발 노드, 도착 노드 그리고 중간 노드를 통해 DP와 유사하게 동작한다.
편의상 이들을 From, To, Middle 이라고 부르자.
0. dist배열의 모든 값을 INF로 초기화한다.
1. 출발 노드와 도착 노드가 같은 경우는 dist값을 0으로 둔다. 즉, i번 노드에 대해 dist[i][i] = 0이다.
2. 그래프에서 주어지는 간선은 dist[From][To] = weight 형태로 저장한다.
(예를 들어, 1번 노드에서 2번 노드로 향하는 가중치 3인 간선은 dist[1][2] = 3 과 같이 저장한다.)
3. 모든 정점을 Middle로 둔 경우들에 대해,
dist[From][To] = min(dist[From][To], dist[From][Middle] + dist[Middle][From])
이는 곧 현재까지 찾은 From 에서 시작하고 To에서 끝나는 최단경로와 (dist[From][To])
From에서 시작하고 Middle에서 끝나는 최단경로(dist[From][Middle]) +
Middle에서 시작하고 To에서 끝나는 최단경로(dist[Middle][To])의 가중치 합을 비교해
더 작은 값으로 갱신한다는 것을 의미한다.

동작 원리 3에 대해 추가적인 설명을 하자면,
가중치 비교의 대상인 dist[From][To]는 단순히 간선의 가중치를 의미하는 것이 아니라
현재까지 찾은 From ~ To의 최단거리이다.
예를 들어 dist[1][4]가 1 -> 2 -> 4 경로의 가중치인 3일 때,
이후에 다른 탐색에서 사용되는 dist[1][4]는 1 -> 2 -> 4의 경로를 내포하고 있는 것이다.
다음의 예제 그래프를 보며 위의 동작 원리를 다시 살펴보자.
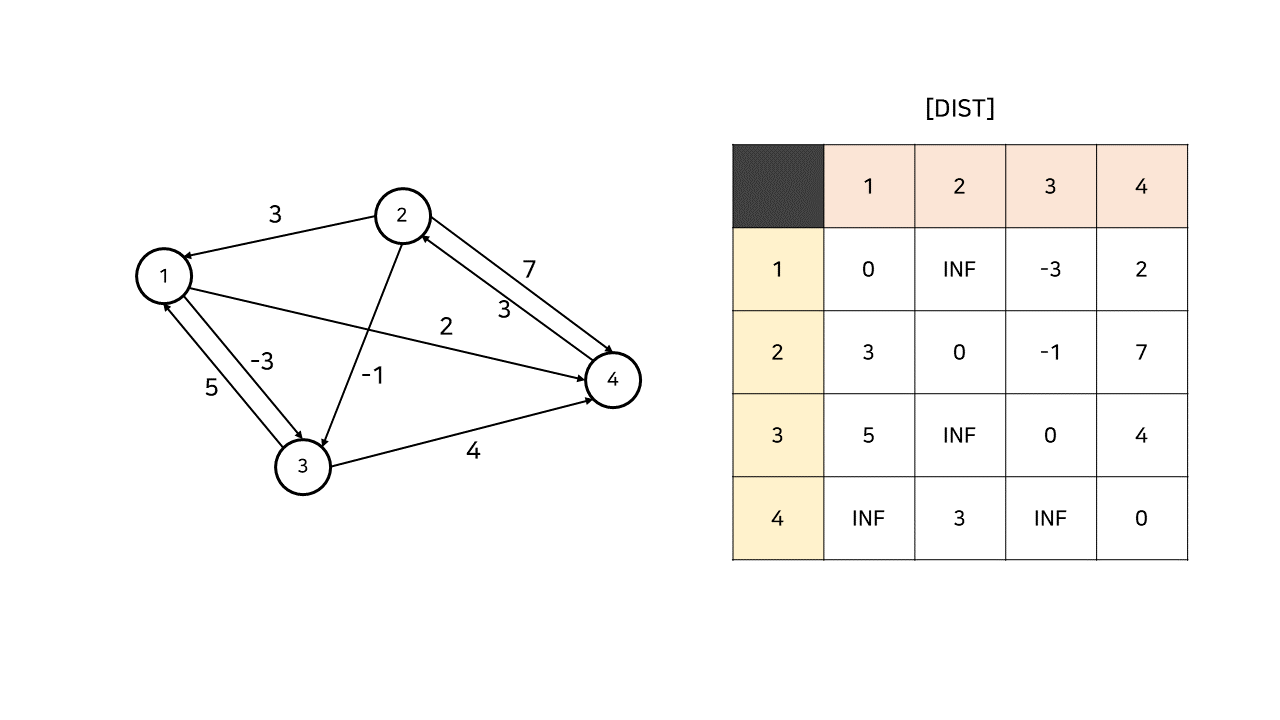
예제 그래프에서 동작 원리 0, 1, 2를 적용한 dist배열은 위와 같다.
각 간선들이 dist 배열의 인덱스에 의해 나타난 것을 확인할 수 있다.
그림에서 노란색은 From, 빨간색은 To, 파란색은 Middle을 의미한다.
플로이드 알고리즘은 모든 노드를 Middle로 두는 경우를 탐색한다.
각각의 Middle 노드에 대해, 모든 (From, To) 쌍의 dist를 비교한다.
우선 Middle = 1일 때, dist 배열의 변화를 살펴보자.
Middle이나 To가 From과 같은 경우는 생략하였다.
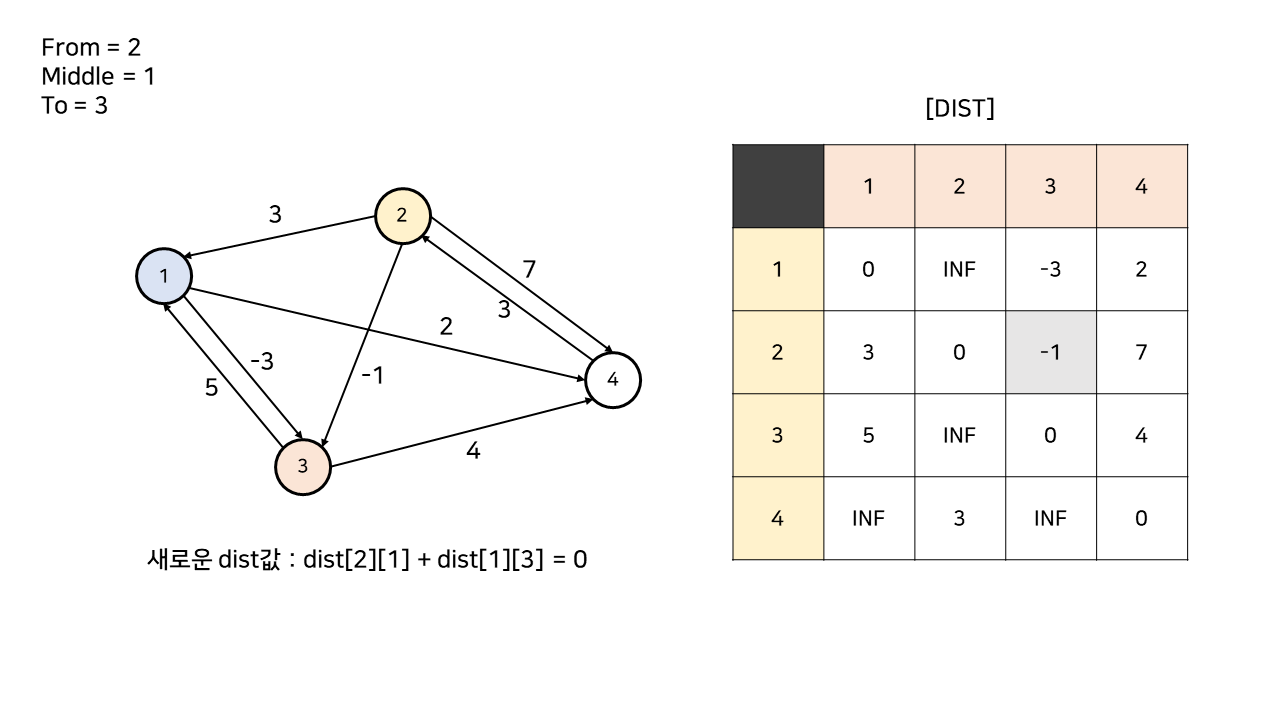
원래 2 -> 3 경로의 가중치인 -1과, 중간 노드인 1번 노드를 거쳐가는 2 -> 1 -> 3 경로의 가중치 0을 비교한다.
중간 노드를 거치는 경로의 가중치가 더 크므로, dist[2][3]은 갱신되지 않는다.
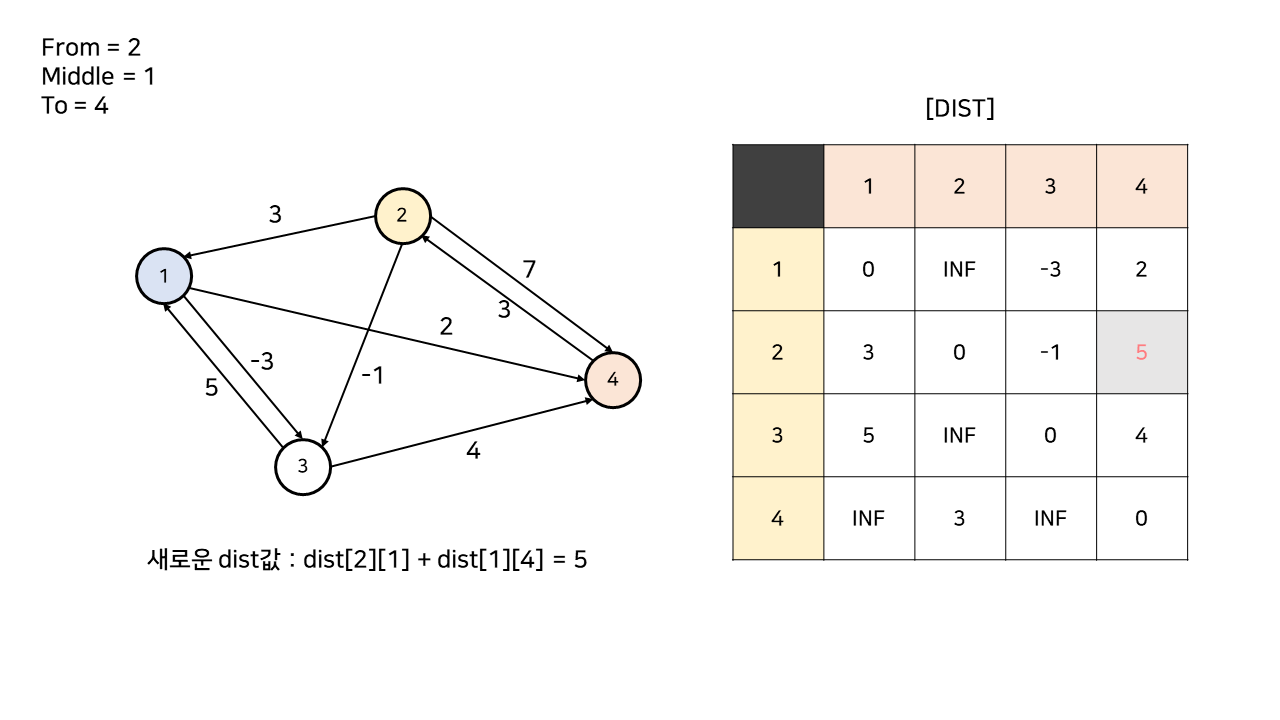
2 -> 4 경로의 가중치가 저장되어 있는 dist[2][4]와
1을 중간 노드로 거쳐가는 2 -> 1 -> 4 경로의 가중치인 dist[2][1] + dist[1][4]를 비교한다.
2 -> 1 -> 4 경로의 가중치가 5로 더 작기 때문에, dist[2][4]는 5로 갱신된다.
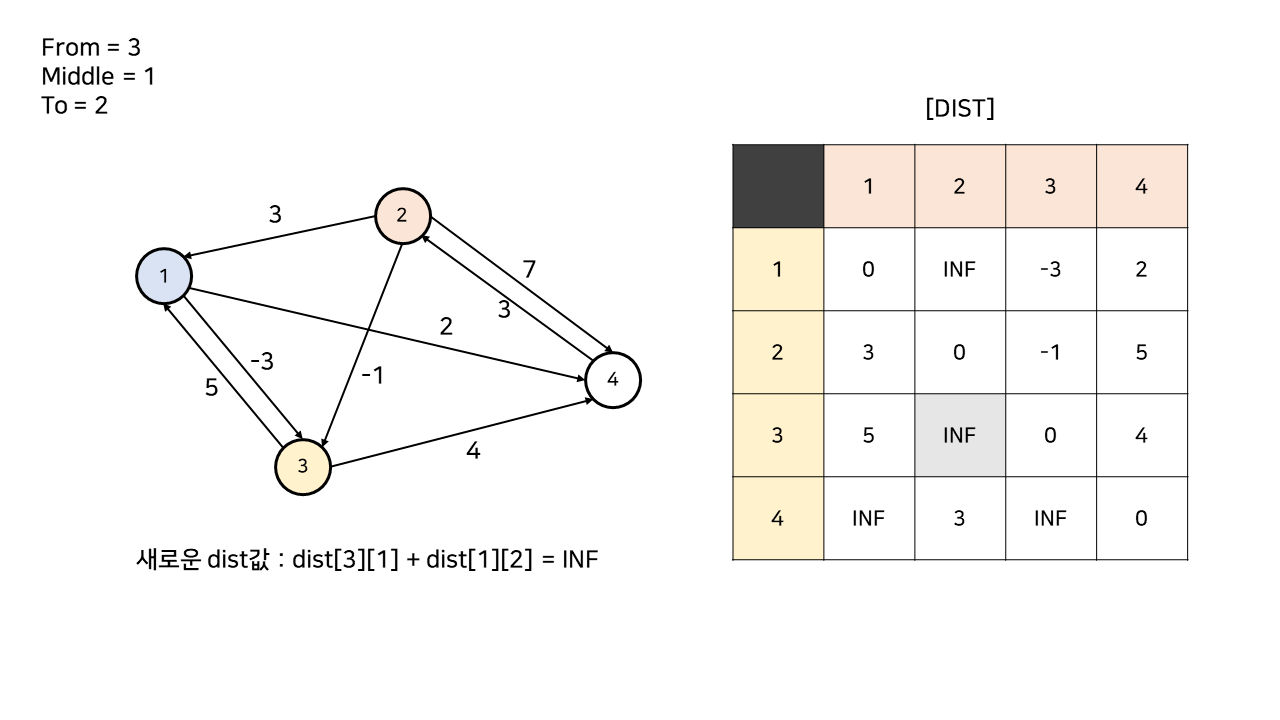
중간 노드인 1에서 2번 노드로 연결된 간선이 현재까진 없으므로, (dist[1][2] = INF)
dist 값을 갱신하지 않는다.

dist[3][1] + dist[1][4]값이 기존 dist[3][4]보다 크므로, 갱신하지 않는다.

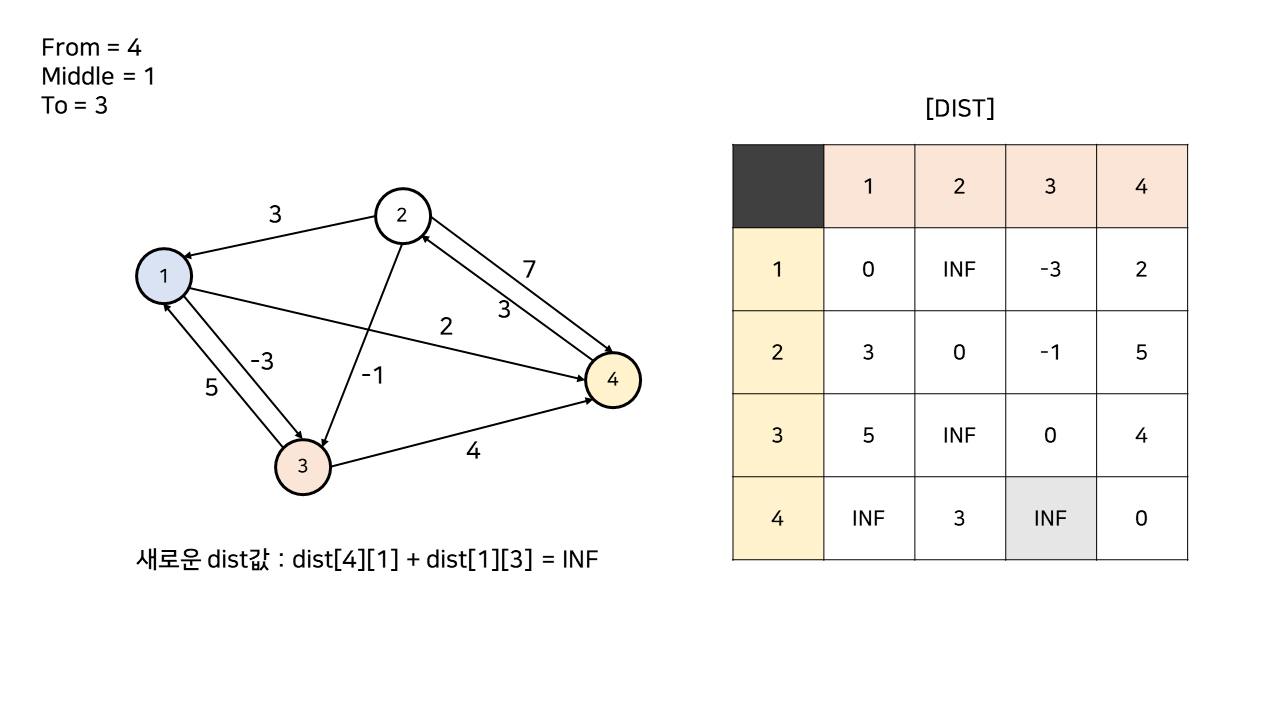
이렇게 한 노드에 대한 중간 노드 루프가 끝났다면, 다음 노드를 중간 노드로 지정해
여태까지의 과정을 반복한다.

위는 2번 노드를 Middle로 정했을 때 dist 배열의 값이 변경되는 한 경우를 나타낸 것이다.
결국 플로이드 알고리즘은, 가능한 모든 경로를 체크하여 모든 최단거리를 구하는 알고리즘이다.

[음의 사이클]
벨만-포드 알고리즘과 마찬가지로 플로이드 알고리즘도 음의 사이클이 존재할 때 최단거리를 구할 수 없다.
벨만-포드 알고리즘에서는 원래의 V - 1번 루프에서 추가적인 루프 진행을 통해 음의 사이클의 존재 여부를 확인했다.
그렇다면 플로이드 알고리즘에서는 음의 사이클을 어떻게 찾아낼 수 있을까?
우리는 동작 원리 1에서, i번 노드에 대해 dist[i][i] = 0으로 초기화했었다.
자기 자신에서 출발해 자기 자신에게 돌아오는 경로의 가중치는 절대 0보다 작아질 수 없기 때문이다.
하지만 그래프에 음의 사이클이 존재한다면, 그 사이클에 포함된 노드를 k라 했을 때 dist[k][k]가 음수 값을 가지게 된다.
따라서, 플로이드 알고리즘을 적용한 후,
모든 노드의 번호 i에 대해 dist[i][i]가 0인지 확인해줌으로써 음의 사이클 존재 여부를 판단할 수 있다.
[구현]
이처럼 체크할 것도 많고, 구하는 것도 다른 최단거리 알고리즘에 비해 가장 많은 플로이드 알고리즘이지만
구현 자체는 다른 알고리즘들에 비해 매우 간단하다. 코드로 살펴보자.
[코드]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
|
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
#include <algorithm>
#define INF 99999999
using namespace std;
typedef pair<int, int> p;
int dist[5][5];
void floyd() {
//각 노드를 middle로 두었을 때,
for (int middle = 1; middle <= 4; middle++) {
//가능한 모든 from, to 쌍에 대해 dist를 갱신한다.
for (int from = 1; from <= 4; from++) {
for (int to = 1; to <= 4; to++) {
dist[from][to] = min(dist[from][to], dist[from][middle] + dist[middle][to]);
}
}
}
}
void init() {
for (int i = 1; i <= 4; i++)
for (int j = 1; j <= 4; j++)
dist[i][j] = INF;
for (int i = 1; i <= 4; i++) dist[i][i] = 0;
dist[1][3] = -3;
dist[1][4] = 2;
dist[2][1] = 3;
dist[2][3] = -1;
dist[2][4] = 7;
dist[3][1] = 5;
dist[3][4] = 4;
dist[4][2] = 3;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(NULL);
init();
floyd();
for (int i = 1; i <= 4; i++) {
for (int j = 1; j <= 4; j++) {
if (dist[i][j] == INF) printf("- ");
else printf("%d ", dist[i][j]);
}
printf("\n");
}
return 0;
}
|
cs |
3중 for문을 돌아 단 4줄만에 알고리즘 구현이 완료된다.
3중 for문의 순서가 middle - from - to 임에 유의하자.
[연습 문제]
BOJ 11404_플로이드 : www.acmicpc.net/problem/11404
11404번: 플로이드
첫째 줄에 도시의 개수 n(1 ≤ n ≤ 100)이 주어지고 둘째 줄에는 버스의 개수 m(1 ≤ m ≤ 100,000)이 주어진다. 그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그
www.acmicpc.net
'알고리즘 > 개념' 카테고리의 다른 글
| 탐욕 알고리즘 (그리디 알고리즘, Greedy Algorithm) (0) | 2020.12.01 |
|---|---|
| 기본 정렬 알고리즘 (Sorting Algorithm) (0) | 2020.11.20 |
| 벨만-포드 알고리즘(Bellman-Ford Algorithm) (0) | 2020.11.01 |
| 다익스트라 알고리즘 (Dijkstra Algorithm) (0) | 2020.10.21 |
| 세그먼트 트리(Segment Tree) (0) | 2020.10.11 |