4Legs_Archives

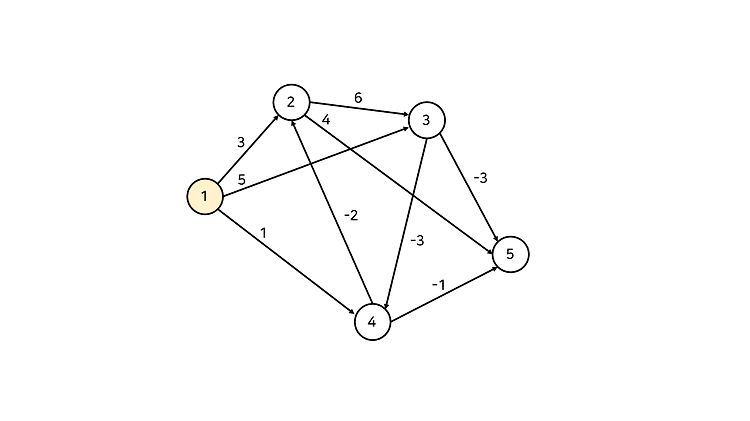
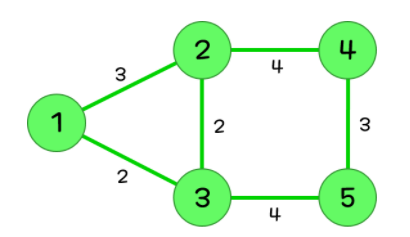
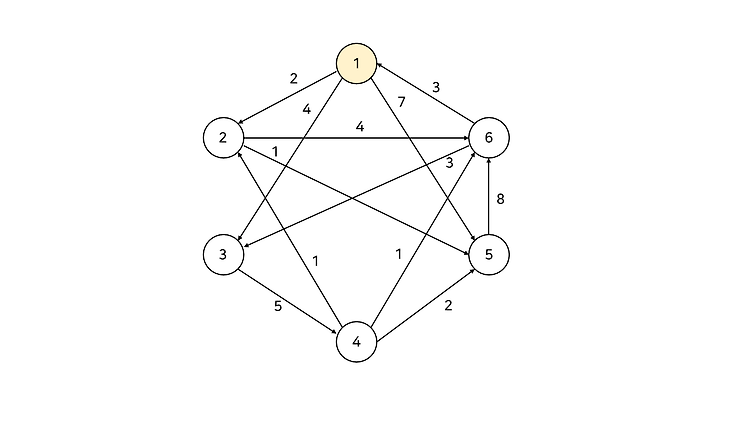
문제 링크 : www.acmicpc.net/problem/1219 1219번: 오민식의 고민 첫째 줄에 도착 도시에 도착할 때, 가지고 있는 돈의 액수의 최댓값을 출력한다. 만약 오민식이 도착 도시에 도착하는 것이 불가능할 때는 "gg"를 출력한다. 그리고, 오민식이 도착 도시에 도착 www.acmicpc.net 벨만-포드 알고리즘에 대한 전반적인 이해가 필요한 문제이다. 이 문제를 막힘없이 해결할 수 있다면 벨만-포드를 잘 이해했다고 볼 수 있을 것이다. 기본적으로는 (도로를 지나며 사용하는 비용 - 도시에 도착해서 벌 수 있는 비용) 을 간선의 비용으로 두는 그래프에 대해 벨만-포드 알고리즘을 적용해 문제를 풀면 된다. (즉 수익의 최대화는 가중치의 최소화가 된다.) 하지만 문제의 조건에서 gg는 오..

문제 링크 : www.acmicpc.net/problem/11657 11657번: 타임머신 첫째 줄에 도시의 개수 N (1 ≤ N ≤ 500), 버스 노선의 개수 M (1 ≤ M ≤ 6,000)이 주어진다. 둘째 줄부터 M개의 줄에는 버스 노선의 정보 A, B, C (1 ≤ A, B ≤ N, -10,000 ≤ C ≤ 10,000)가 주어진다. www.acmicpc.net 벨만-포드 알고리즘을 이해하고 연습해볼 수 있는 문제이다. 벨만-포드 알고리즘에 대해서는 다음 포스트를 참조하자. 벨만-포드 알고리즘(Bellman-Ford Algorithm) [서론] 벨만-포드 알고리즘은 다익스트라 알고리즘과 마찬가지로 한 정점에서 출발하여, 다른 모든 정점에 대한 최단경로를 구하는 알고리즘이다. (다익스트라 알고리즘..

[서론] 벨만-포드 알고리즘은 다익스트라 알고리즘과 마찬가지로 한 정점에서 출발하여, 다른 모든 정점에 대한 최단경로를 구하는 알고리즘이다. (다익스트라 알고리즘 : 4legs-study.tistory.com/21) 하지만, 다익스트라 알고리즘에는 그래프에 음의 가중치가 없어야 한다는 조건이 있었다. 왜일까? 음의 가중치를 가진 간선이 존재한다면, 힙에서 한 정점을 꺼냈을 때 그 가중치 합이 해당 정점에 대한 최소 가중치 합임을 보장할 수 없기 때문이다. 다익스트라 알고리즘은 힙에서 꺼낸 정점에 대해 꺼낸 순간의 가중치 합을 최소로 고정한 후 (음의 가중치가 없다면 다른 어떤 간선을 추가로 지나오더라도 현재 가중치 합보다 작아질 수 없으므로) 다른 정점에 대해 해당 과정을 반복하는데, 음의 가중치를 가진..

문제 링크 : www.acmicpc.net/problem/1854 1854번: K번째 최단경로 찾기 첫째 줄에 n, m, k가 주어진다. (1 ≤ n ≤ 1000, 0 ≤ m ≤ 2000000, 1 ≤ k ≤ 100) n과 m은 각각 김 조교가 여행을 고려하고 있는 도시들의 개수와, 도시 간에 존재하는 도로의 수이다. 이어지는 m개의 줄에 www.acmicpc.net 다익스트라 알고리즘을 적용해 각 정점에 대한 K번째 최단경로의 가중치 합을 구하는 문제이다. 일반적인 다익스트라 알고리즘에서는 우선순위 큐(최소 힙)에서 pop되는 순간 그 정점에 대한 최소 가중치 합은 고정된다. (다익스트라 알고리즘 참조 : 4legs-study.tistory.com/21) 다익스트라 알고리즘은 기본적으로 최단거리를 구하..

문제 링크 : www.acmicpc.net/problem/1162 1162번: 도로포장 첫 줄에는 도시의 수 N(1 ≤ N ≤ 10,000)과 도로의 수 M(1 ≤ M ≤ 50,000)과 포장할 도로의 수 K(1 ≤ K ≤ 20)가 공백으로 구분되어 주어진다. M개의 줄에 대해 도로를 연결짓는 두 도시와 도로를 통과하 www.acmicpc.net 어떠한 도시에 도착했을 때, 몇 개의 도로를 포장해서 이동했는지는 구별되어야 한다. 이전 포스팅인 BOJ16118_달빛 여우 문제처럼 가중치에 어떤 요소가 더해졌을 때는 이를 구별하기 위해 DP를 섞어 사용한다. 따라서, dist 배열을 dist[n][k]와 같은 이차원 배열 형태로 구성해 문제를 해결하자. dist[i][j] = i번 도시에 j개의 도로를 포장..

문제 링크 : www.acmicpc.net/problem/16118 16118번: 달빛 여우 첫 줄에 나무 그루터기의 개수와 오솔길의 개수를 의미하는 정수 N, M(2 ≤ N ≤ 4,000, 1 ≤ M ≤ 100,000)이 주어진다. 두 번째 줄부터 M개의 줄에 걸쳐 각 줄에 세 개의 정수 a, b, d(1 ≤ a, b ≤ N, a ≠ b www.acmicpc.net 가중치를 번갈아 x2, /2 하여 이동하도록 하는 다익스트라 알고리즘을 구현하는 문제이다. 우선 가중치의 /2에 값이 유실되지 않도록 그래프의 가중치는 입력값의 2배로 설정한다. 기존 다익스트라 알고리즘의 우선순위 큐에 인자를 추가하여, (이 풀이에선 sprint 이다.) 해당 인자의 값에 따라 다익스트라 내의 새 dist에 x2 또는 /2..

문제 링크 : www.acmicpc.net/problem/9370 9370번: 미확인 도착지 (취익)B100 요원, 요란한 옷차림을 한 서커스 예술가 한 쌍이 한 도시의 거리들을 이동하고 있다. 너의 임무는 그들이 어디로 가고 있는지 알아내는 것이다. 우리가 알아낸 것은 그들이 s지점에서 www.acmicpc.net 결국 문제는 특정한 하나의 간선을 출발지로부터의 최단경로에 포함하는 노드들을 구하는 것이다. 후술할 다른 풀이방법도 있지만, 문제의 의도에 따라 다익스트라 알고리즘을 적용해 정석으로 풀이해보자. 위의 예제 그래프에서 2번 노드에서 어떤 목적지 후보 노드에 대한 최단경로가 1-3 간선을 포함하고 있다면, 1번 노드에서 그 목적지 후보 노드에 대한 최단거리는 출발 노드로부터 목적지 후보 노드까지..

[서론] 그래프 최단경로 알고리즘으로, 꽤 자주 보이는 유형이다. 다익스트라 알고리즘은 음수가 아닌 가중치가 있는 그래프에서 한 점으로부터 다른 모든 점까지의 최단 경로를 구하는 알고리즘이다. [동작 원리] 다음과 같은 그래프에서, 1번 노드와 나머지 각 노드 간의 최단거리를 다익스트라 알고리즘을 통해 구해보자. 다익스트라 알고리즘은 위와 같은 상태에서 시작한다. 테이블의 값은 출발 노드로부터 해당 노드까지의 최소 가중치 합을 의미하며, 테이블의 값이 INF(무한대)라면 해당 노드와 연결되어 있지 않다는 의미이다. 아직은 1번 노드만 확인했으므로, 다른 모든 노드에 대해 INF가 기록된 모습이다. 출발 노드로부터 인접한 각 노드에 대해 테이블에 거리를 기록한다. 예시 그래프에서는 출발 노드 1이 2, 3..

문제 링크 : www.acmicpc.net/problem/1422 1422번: 숫자의 신 첫째 줄에 K와 N이 공백을 사이에 두고 주어진다. K와 N은 각각 1,000보다 작거나 같은 자연수이고, N은 K보다 크거나 같다. 둘째 줄에는 K개의 수가 한 줄에 하나씩 주어진다. 각 수는 1,000,000,000보�� www.acmicpc.net 예전에 풀었던 DP 문제인 '방번호' 문제와 비슷한 맥락의 문제이다. 가장 큰 수를 만들기 위해선, 각 숫자들을 최소 한 번씩 사용해야 하므로 숫자의 앞자리가 큰 순으로 붙여나간다. 각 숫자들을 최소 한 번씩 사용하고 난 뒤, 추가로 사용할 숫자는 가장 큰 수가 될 것이다. 즉, 입력으로 들어오는 숫자들을 어떻게 정렬할 것인지가 문제의 핵심이 된다. 추가로 사용할 숫..

문제 링크 : www.acmicpc.net/problem/1256 1256번: 사전 첫째 줄에 N, M, K가 순서대로 주어진다. N과 M은 100보다 작거나 같은 자연수이고, K는 1,000,000,000보다 작거나 같은 자연수이다. www.acmicpc.net 중복조합과 관련된 dp문제이다. a와 z를 통해 문자열을 만드는 것은 다음과 같이 생각할 수 있다. i개의 a에 대해 바깥 공간을 포함한 사이 공간들에 j개의 j를 넣는 것으로 생각하면, j개의 z를 i+1개의 공간에 넣는 가짓수가 된다. 따라서, iHj가 곧 구하는 만들 수 있는 총 문자열의 갯수가 된다. 중복조합을 계산하기 위해서는 팩토리얼이 섞인 식을 계산해야 하는데, 이 부분에서 dp를 활용할 수 있다. 굳이 증명하자면 중복조합은 다음과..