4Legs_Archives

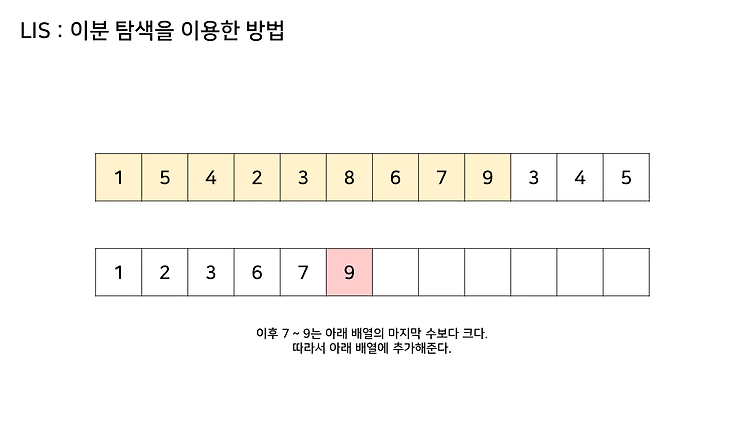
문제 링크 : www.acmicpc.net/problem/11054 11054번: 가장 긴 바이토닉 부분 수열 첫째 줄에 수열 A의 크기 N이 주어지고, 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ N ≤ 1,000, 1 ≤ Ai ≤ 1,000) www.acmicpc.net 최장 증가 수열(LIS)에 대해 숙지하고 있다면 쉽게 해결할 수 있는 문제이다. 전체 수열의 크기가 1000으로 작기 때문에 O(N^2)의 시간복잡도를 갖는 DP를 사용할 수 있다. 수열의 한 수에 대해, 왼쪽 끝에서 그 수에서 끝나는 LIS와 오른쪽 끝에서 시작해 그 수에서 끝나는 LIS 길이의 합(-1)이 곧 바이토닉 수열의 길이가 된다. (이 때, 원래의 수는 그 바이토닉 부분 수열에서 가장 큰 값이 된다.) ..

최장 증가 수열 (LIS, Longest Increasing Subsequence) 최장 증가 수열, 정확히 최장 증가 부분 수열은 어떠한 수열에서 오름차순으로 증가하는 가장 긴 부분수열을 의미한다. 이 때, 부분 수열의 각 수는 서로 연속할 필요는 없다. 아래의 예시 수열을 보자. 위 수열에서 최장 증가 수열을 찾으면 아래와 같다. 그림에서 붉은 칸으로 칠해진 부분 수열 (1, 2, 3, 6, 7, 9) 는 전체 수열 중 오름차순으로 증가하는 가장 긴 부분수열이다. 이제 주어진 수열에서 LIS의 길이를 구하는 두 가지 방법을 알아보자. 다이나믹 프로그래밍을 이용한 방법 : O(N^2) 이러한 최장 증가 수열을 찾는 가장 단순한 방법은 완전 탐색일 것이다. 하지만 수열에 존재하는 수의 개수가 k개일 때,..

문제 링크 : www.acmicpc.net/problem/13141 13141번: Ignition 첫 번째 줄에는 그래프의 정점의 수 N과 간선의 수 M이 주어진다. (2 ≤ N ≤ 200, N-1 ≤ M ≤ 20,000) 두 번째 줄부터 M개의 줄에는 각 간선의 시작점 S, 끝점 E, 길이 L이 주어진다. (1 ≤ L ≤ 100) 시작점 www.acmicpc.net 간선들은 그 간선의 양 끝 노드에 불이 옮겨진 순간부터 타는 시간이 절반으로 줄어들게 된다. 쉽게 설명하자면 다음 그림과 같다. 정점 A에 불이 먼저 붙은 상황이다. 이 때, A와 B를 잇는 간선은 A쪽에서 먼저 타게 된다. B쪽에는 아직 불이 도착하지 않았기 때문이다. 이제 정점 B에도 불이 붙었다. 이제는 간선의 남은 길이가 양쪽에서 타..

문제 링크 : www.acmicpc.net/problem/8984 8984번: 막대기 첫 줄에는 막대기의 개수와 수평선 사이의 간격을 나타내는 두 개의 정수 N과 L이 주어진다. 여기서 N은 1 이상 100,000 이하이고, L은 1 이상 1,000,000 이하이다. 그 다음 N 개의 줄에는 각 줄마다 막대 www.acmicpc.net 위쪽 수평선의 한 점과 아래쪽 수평선의 서로 다른 10개의 점을 잇는 막대기가 있는 상황을 가정해 보자. 이들 중 가장 긴 막대기를 선택한다고 해서, 가장 긴 지그재그가 나올지는 알 수 없다. 따라서 이 문제는 그리디 알고리즘이 아닌 다이나믹 프로그래밍으로 접근해야 한다. 어떤 한 막대에서 지그재그가 끝난 상황을 생각해 보자. 이 때, 맨 마지막 막대를 기준으로 지그재그는..

문제 링크 : www.acmicpc.net/problem/2211 2211번: 네트워크 복구 첫째 줄에 두 정수 N, M이 주어진다. 다음 M개의 줄에는 회선의 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 컴퓨터와 B번 컴퓨터가 통신 시간이 C (1 ≤ C ≤ 10)인 회선으로 연결되어 있다 www.acmicpc.net 문제를 자세히 읽지 않는다면 최소 스패닝 트리(MST) 문제로 혼동할 수 있다. 제시된 조건 중, "따라서 슈퍼컴퓨터가 다른 컴퓨터들과 통신하는데 걸리는 최소 시간이, 원래의 네트워크에서 통신하는데 걸리는 최소 시간보다 커져서는 안 된다." 라는 내용이 있기 때문에 이 문제는 최소 스패닝 트리로 해결할 수 없게 된다. 다음과 같은 반례를 들 수 있다. 그림에서 붉은 색으..

문제 링크 : www.acmicpc.net/problem/2560 2560번: 짚신벌레 첫째 줄에 a, b, d, N을 나타내는 네 정수가 빈칸 하나를 사이에 두고 차례로 주어진다. 단, 0＜a＜b＜d≤10,000이고, 1≤N≤1,000,000이다. www.acmicpc.net 문제를 간단하게 생각해야 깔끔하게 점화식을 구할 수 있다. "dp[k] = k일째 되는 날의 짚신벌레 개체 수"로 두고 문제를 풀어보자. 우선, 예제인 a = 2인 상황에서 짚신벌레가 증식만 한다고 가정한다면 다음과 같다. 0일째 되는 날: (0) 1일째 되는 날: (1) 2일째 되는 날: (2, 0) 3일째 되는 날: (3, 1, 0) 4일 째 되는 날: (4, 2, 1, 0, 0) 5일 째 되는 날: (5, 3, 2, 1, 1..

문제 링크 : www.acmicpc.net/problem/3665 3665번: 최종 순위 올해 ACM-ICPC 대전 인터넷 예선에는 총 n개의 팀이 참가했다. 팀은 1번부터 n번까지 번호가 매겨져 있다. 놀랍게도 올해 참가하는 팀은 작년에 참가했던 팀과 동일하다. 올해는 인터넷 예선 본부에 www.acmicpc.net 순위의 개념을 그래프에 위상 정렬을 적용하여 나타낼 수 있는가를 묻는 문제이다. 다만 초반 그래프를 구성하는 것이 다소 까다롭다. 위상 정렬 (Topological Sort) 위상 정렬 (Topological Sort) 방탈출 게임을 한다고 생각해 보자. 우리는 메인 룸에 있는 3개의 자물쇠를 풀어야 탈출에 성공하고, 다음 단계의 탈출에 도전할 수 있다. 3개의 열쇠는 메인 룸과 연 4le..

문제 링크 : www.acmicpc.net/problem/11266 11266번: 단절점 첫째 줄에 두 정수 V(1≤V≤10,000), E(1≤E≤100,000)가 주어진다. 이는 그래프가 V개의 정점과 E개의 간선으로 이루어져 있다는 의미이다. 다음 E개의 줄에는 간선에 대한 정보를 나타내는 두 정수 A, B www.acmicpc.net 그래프의 단절점이란, 그래프에서 한 정점을 제거했을 때 그래프의 Connected Component가 증가하는 정점을 말한다. Connected Component는 DFS, BFS 등으로 그래프를 탐색했을 때 한 덩어리로 묶이는 정점들의 집합이라 이해하면 된다. 즉 그래프의 모든 정점을 발견하는 데 실행되는 탐색의 횟수와도 같다. 다음 그래프를 통해 단절점의 특징을 파..

문제 링크 : www.acmicpc.net/problem/15562 15562번: 네트워크 우리의 회사에는 N개의 네트워크 시스템 S1, S2, ..., SN와 이들을 연결하는 M개의 네트워크들 W1, W2, ..., WM이 있다. 네트워크 시스템들은 우선순위가 있어 모든 네트워크는 우선순위가 www.acmicpc.net 임의의 시스템 K에 대해 다음과 같은 경우를 생각해보자. 이 경우, 문제의 조건에 따라 네트워크를 정리하면 다음과 같다. 만약 K에서 B ~ F로 각각 나가는 간선이 하나씩 존재하더라도, 이 간선들은 모두 A에서 B ~ F로 나가는 간선으로 대체될 수 있다. 즉, 한 노드를 기준으로 자신에게 들어오는 간선이 존재한다면, 자신에게서 나가는 간선들은 위의 A -> B와 같이 대체될 수 있다..

문제 링크 : www.acmicpc.net/problem/2437 2437번: 저울 하나의 양팔 저울을 이용하여 물건의 무게를 측정하려고 한다. 이 저울의 양 팔의 끝에는 물건이나 추를 올려놓는 접시가 달려 있고, 양팔의 길이는 같다. 또한, 저울의 한쪽에는 저울추들만 놓 www.acmicpc.net 주어진 무게추로 측정할 수 없는 최소무게를 구하는 문제이다. 무게추 1, 2, 3을 갖고 있다고 가정할 때, 우리는 1에서 6까지의 모든 무게를 측정할 수 있다. 이 상태에서 새로운 무게추 5가 추가되었을 때, 이미 우리는 1에서 6까지의 무게를 1~3 무게추로 측정할 수 있었기 때문에 각 무게에 대한 무게추 조합에 5 무게추만 추가한 새로운 조합을 만들어 낼 수 있다. 다시 말해 우리가 2, 3 무게추를 ..